Quando si tratta di sostenibilità è comunemente accettato che se ne debbano considerare non solo gli aspetti relativi all’ambiente, ma anche quelli che coinvolgono l’economia e l’impatto sulla società. Questi tre “pilastri” della sostenibilità sono alla base delle specifiche norme europee e devono essere presi in conto anche per i materiali da costruzione, caso in cui un approccio volutamente banalizzato, usato talvolta per impressionare i non specialisti, può portare a conclusioni fuorvianti se non del tutto errate.
Per i tre più diffusi materiali da costruzione – legno, acciaio e calcestruzzo armato – nell’articolo vengono esaminati alcuni aspetti relativi ai tre “pilastri” citati: per il sociale, la sicurezza degli individui, per l’ambientale le emissioni di CO2 e per l’economico i costi. L’intento è di separare i “fatti” dai “miti” intendendo come tali quelle idee che suonano così ragionevoli da essere universalmente accettate anche se basate su ipotesi talvolta errate.
Definito il concetto di “unità funzionale” si sviluppa il confronto per una unità semplice, un pilastro dimensionato seguendo le regole di progetto della specifica norma europea di calcolo, il relativo Eurocodice. Per un materiale non omogeneo come il calcestruzzo armato vengono definiti gli opportuni “coefficienti di incremento” delle prestazioni del solo calcestruzzo che tengono conto della presenza dell’armatura. Per finire si esamina cosa cambia passando dai casi ideali ai casi reali e se si considerano altri tipi di unità funzionali.
L’articolo è in lingua inglese.
A MYTH: THE STRENGTH/SPECIFIC WEIGHT RATIO
The following is taken from lesson slides about timber structural design given in an Italian University.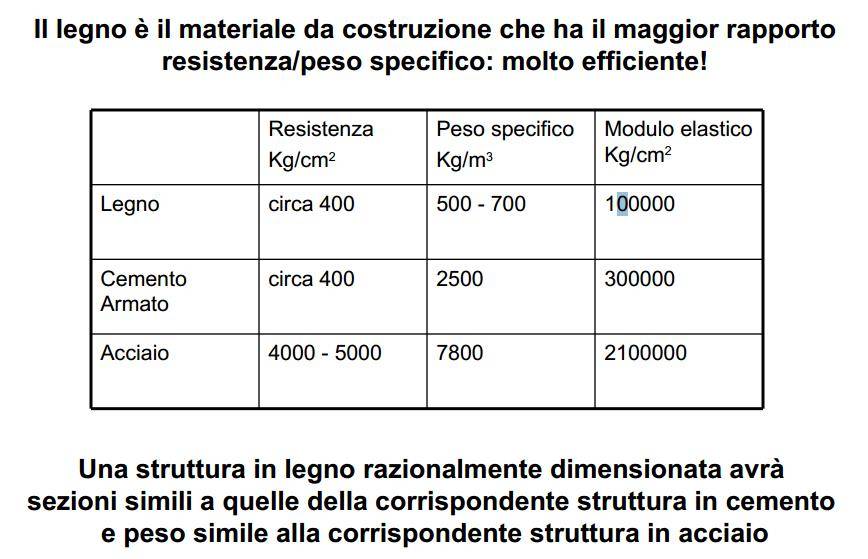
The table gives average values of compressive strength (“resistenza”), specific weight (“peso specifico”) and elastic modulus (“modulo elastico”) of three materials, timber (“legno”), steel (“acciaio”) and reinforced concrete (“cemento armato”). The sentence above the table says: “Timber is the construction material with the highest strength/specific weight ratio: very efficient!”. The sentence below says “A well-designed timber structure has a similar section to one with (reinforced) concrete, and weight similar to a steel one”. As written, the two sentences address two different questions. The first one based on materials alone states that the “efficiency” of materials should be measured – and therefore materials compared - on the basis of their (compressive) strength/specific weight ratio; the second considers the impact of materials in designing a structure.
At first sight the strength/specific weight ratio criterion sounds good – the lighter and stronger the material, the better. But what does this mean when compressive strength is used, as in the table? In this case it may be considered a myth – it sounds convincing, but misleading if we go into detail. The underlying idea is to build an ideal column of constant section A as high as the (compressive) strength of a material allows and to assess materials’ efficiency on the basis of “the greater the height , the better the material”.
Let’s define “f” the collapse strength (compressive load per unit area) of a generic material, and “A” the area of its transverse section: the maximum load F the area A can withstand when uniformly loaded (as in a column subject to a theoretically perfectly axial load) is F = (f A). The weight W of a column of height “h” is obtained by multiplying its volume V = (Ah) by w, the specific weight of the material, so W = w V = w (A h). Equating the “resistance” F and the “action” W the height hmax equals the (compressive) strength/specific weight ratio:
F= W --> f A = w A hmax --> hmax = (f/w)
Expressing the strength in kg/m2 and hmax in meters, using initials “s” for steel, “c” for concrete and “t” for timber and the data in the table:
hmax,s = (4000x104)/7850 = 5100 m
hmax,c = (400x104)/2500 = 1600 m
hmax,t = (400x104)/500 = 8000 m
On the basis of this easily understood, easily calculated “performance” criterion, timber scores best of the three: a really attractive construction material! But something must be wrong or missing in this approach if in the real world the tallest building constructed with concrete, Burj Dubai, is “only” 830 m high, the tallest building made of steel, Taipei 101, is “only” 501 m high and the world’s tallest building made of timber (the most “efficient” construction material according to this criterion) is of 12 timber storeys supported by 3 concrete storeys, built for the EXPO 2015 in Milan (IT). And Hyperion, the tallest tree in the world, a “sequoia sempervirens” in California Redwood National Park is “only” 116 m high! With computers available today why are our engineers (even the best among engineers, Mother Nature) still unable to cope with the intrinsic properties of construction materials? Is it their fault, or is the strength/specific weight ratio, i.e. the maximum theoretical height hmax a misleading indicator, a “myth”?
Let’s look at some “facts”. In the structural design of even the simplest structure like an ideal column, correct figures have to be used: the compressive strength of all three materials is in reality not a single figure as in the table above, but a range of strengths “fk” (the subscript k means “characteristic”, i.e. a single figure evaluated on a statistical basis). These fk values identifying the “strength class” of each material are defined in the relevant product standard and referred to in the relevant design standard (in Europe, in Eurocodes). As a structure designed on the basis of a material characteristic strength would have too high a probability of collapse, engineers use a value lower than the characteristic strength fk of the material - its “design” strength fd = fk/gm (d = “design”). This is obtained by dividing “characteristic” values by the material-specific “safety factor”, gm, which takes into account both material and design issues - how the material is manufactured, how material properties are influenced by the environment, how accurate are the theoretical models used in design etc. Safety factors, gm, may differ from country to country, but max-min values can be easily identified. Dealing with columns in compression, the ranges of characteristic compressive strengths fk, the appropriate safety factors, the compressive design strengths, fd, and other (partly amended) mechanical properties of materials are listed in table 1 for the three materials.
Material | Mean density rmean | Character. compression strength fk | Safety factor g | Design strength fd | hmax = fd /w | Slenderness ratio l | Slenderness
radius
h/l |
| kg/m3 | N/mm2 | - | N/mm2 | m | - | m |
Timber | 350 - 550 | 19 – 29 | 2,40 | 7,9 -12,0 | 2025 – 2210 | 20 | 101 - 111 |
Concrete | 2300-2400 | 20 – 55 | 1,4 -1,5 | 13,3 – 36,7 | 566 - 1560 | 50 | 11 - 31 |
Steel | 7850 | 390 – 550 | 1,05 | 224 - 524 | 2850 - 6670 | 150 | 19 - 45 |
Table 1. Material properties, height hmax and slenderness radius
If the ranges of maximum heights are re-calculated on the basis of the design strengths, the previous picture is reversed (table 1): steel comes first, then timber and concrete. Though now more realistic, the new maximum height values remain remote from the real world, so something is still missing.
The first rule for the sustainable use of any material is to reduce the quantity of material required to an absolute minimum. As engineers say, “structures are designed from top to bottom” (and usually built from bottom to top) because going down, from top to bottom, the total weight W of the structure - and the service loads it supports, if any - obviously increase. Given a maximum material strength, fd, the area of the structure, A, should therefore not be constant but increase from a theoretical minimum at the top to a maximum Amax in the bottom. The geometry of this “uniform resistance column” with (variable) section area A is well known and may be easily recognized in a number of man-made and natural structures.
With this variable area A the weight W is reduced, and the height hmax should increase, so the problem remains: with can even a uniform resistance column not reach the theoretical maximum height hmax? Answer: because it would be too “slender” and collapse due to instability - as the Tower of Babel did. This “buckling attitude” is taken into account in design standards by setting limits to the “slenderness ratio”, l, of the material. For an ideal column of constant circular shape of radius r, i.e. with no preferred buckling direction, this is:
l= K h/r --> r = K h/l
K is a parameter which depends on the effectiveness of the restraints at the extremities of the column and, in a simplified analysis, K = 1,0 may be assumed for all materials, i.e. not to depend on the material.
For a given height h the greater the slenderness ratio l, the lower the radius and the area A, so the lower the quantity of material required - and vice versa. The h/l parameter therefore takes into account both strength and stability, two aspects to be considered in the case of columns.
On the basis of the maximum heights hmax previously calculated and the limit values for l given in the relevant Eurocode for timber, (reinforced) concrete and steel, slenderness radii (h/l) have been calculated (table 1). On the basis of (h/l) concrete scores first and while there is no significant difference between concrete and steel, timber has a (h/l) value significantly higher than that of the other two. This is one of the reasons why the highest building in the world is made of concrete and the height of real timber structures is limited : buckling is a problem for this material.
Taking into account “facts” it is evident that for construction materials the (compressive) strength to specific weight ratio is misleading when structures have to sustain compression loads. It makes sense for other type of structures – rockets, ships, airplanes, Formula 1 racing cars, bridges – where weight is really THE problem. This is the reason why light alloys like aluminium were used in the past and composite materials such as carbon fibres are used today. The situation will probably change in the future, due to the advance of science and technology which will give us stronger but lighter construction materials, but today facts are as described.


