Sismabonus 2017: riflessioni, contributi grafici ed esempi

L'articolo esamina alcuni aspetti dei due metodi (convenzionale e semplificato) introdotti dalle Linee Guida per la classificazione del rischio sismico delle costruzioni emanate il 28 febbraio 2017 dal Ministero delle Infrastrutture e dei Trasporti, cercando di evidenziarne le peculiarità. Vengono forniti anche dei contributi grafici ed analitici che possono risultare utili sia nelle applicazioni pratiche, sia per comprendere meglio il ruolo dei parametri in gioco.

 

Sisma Bonus e Classificazione del Rischio Sismico

Questo lavoro è diviso in due parti.

La prima contiene alcune considerazioni di tipo generale, relative al contesto nel quale si inseriscono le Linee Guida per la Classificazione del Rischio Sismico delle Costruzioni [1] allegate al D.M. 28 febbraio 2017, n. 58, del Ministero delle Infrastrutture e dei Trasporti e s.m.i. [2] (in seguito chiamate, per brevità, Linee Guida per la classificazione o anche, semplicemente, Linee Guida).

Nella seconda parte vengono forniti alcuni contributi di carattere operativo che possono risultare utili per avere maggiore evidenza su come influiscono i diversi parametri (essenzialmente l’indice di sicurezza IS-V e l’indice di rischio per lo stato limite di danno, I_{R SLD}). In appendice vengono poi ricordati gli aspetti probabilistici su cui si basa la metodologia in questione.

Quanto di seguito illustrato con riferimento al metodo convenzionale vale per qualsiasi tipologia costruttiva, mentre gli esempi svolti ed il confronto con il metodo semplificato riguardano in modo specifico le costruzioni in muratura.

La CLASSIFICAZIONE SISMICA: un approccio di TIPO CONVENZIONALE

Un primo elemento su cui è opportuno soffermarci è che la classificazione indicata dalle Linee Guida è di tipo convenzionale, nel senso che costituisce un modello con un percorso prefissato, che tutti devono seguire adottando le stesse regole operative. L’obiettivo, evidentemente, è quello di garantire la confrontabilità e l’uniformità – dal punto di vista metodologico - degli esiti.

In realtà non è proprio così, neppure per il metodo chiamato proprio “convenzionale”, perché, in certi casi, per edifici in condizioni del tutto analoghe si possono ottenere risultati anche molto diversi.

Ad esempio, costruzioni con uguale indice di sicurezza IS-V dovrebbero essere, per quanto riguarda il sismabonus, in condizioni simili. Se tutti usassero il valore “standard” di η = 1/0,41 previsto nelle Linee Guida in effetti sarebbe così, ma se invece si sfrutta la possibilità di assumere η differenti a seconda della zona sismica nella quale si trova la costruzione, allora si possono avere esiti diversi.

Per rendersene conto basta considerare, a puro titolo di esempio, tre edifici che hanno lo stesso indice di sicurezza, ad esempio: IS-V = PGA_C/PGA_D = 0,4, ma si trovano in tre diverse città: Cosenza (zona 1), Perugia (zona 2) e Milano (zona 3).

Se utilizziamo le curve di pericolosità (Figura 1) delle tre diverse località (ricavabili facilmente tramite applicazioni software disponibili in rete, basate peraltro sulle tabelle contenute nelle NTC) si vede come, per quello stesso valore del rapporto PGA_C/ PGA_D relativamente allo SLV, si trovino valori diversi del periodo di ritorno (T_R = 33, 47, 66) e quindi delle frequenze di ricorrenza λ.   

Ciò deriva, come evidente nella Figura 1, dalla diversità delle curve: le PGA_C relative allo SLV corrispondenti al 40% delle diverse PGA_D sono differenti e ad esse corrispondono periodi di ritorno diversi, ordinati in modo coerente con i valori delle PGA_D (a PGA_D maggiore corrisponde un maggiore periodo di ritorno per la PGA_C).

Per valutare tale parametro, le Linee Guida indicano la possibilità, “in assenza di più specifiche valutazioni” (ovvero se non si considerano le curve di pericolosità di cui sopra) di passare dalle PGA ai periodi di ritorno utilizzando la seguente espressione:

T_RC = T_RD * (PGA_C / PGA_D) ^η                                                                                                                       (1)

Nella (1) si può inserire il valore standard indicato dalle Linee Guida, ovvero η  = 1/0,41, oppure si possono utilizzare valori di h diversi a seconda dell’accelerazione di picco relativa al sito in esame:

η = 1/0,49    per  a_g > 0,25g;   

η = 1/0,43    per  0,25g ≥ a_g >0,15g;  

η = 1/0,356  per  0,15g ≥ a_g >0,05g;  

η = 1/0,34    per  0,05 g ≥ a_g

Come si vede, η  = 1/0,41 è, più o meno, il valore medio dei diversi η.

Nel caso in esame, si ha T_R = 32, 56 e 73 rispettivamente per l’edificio a Milano (η = 1/0,34), Perugia (η = 1/0,43) o Cosenza (η = 1/0,49), invece di T_R = 51 che si avrebbe con η = 1/0,41 o dei valori T_R = 33, 47, 66 che si troverebbero attraverso le curve di pericolosità prima considerate (Figura 1).

Tutto questo porta a frequenze λ_SLV differenti a seconda della strada scelta ed introduce così una notevole “elasticità” nell’applicazione della procedura, portando, come vedremo negli esempi riportati al successivo punto 4, a risultati anche molto diversi tra loro. 

METODO CONVENZIONALE: Contributi grafici alla PROCEDURA OPERATIVA

Il metodo convenzionale è descritto in modo chiaro ed esauriente nelle Linee Guida e peraltro sono già usciti vari contributi [3][4][5][6] che illustrano quel testo.

Va detto anche che il calcolo dell’indice PAM, così come indicato nelle Linee Guida è molto semplice ed immediato, basta tenere conto di alcune regole di base. Non ci sarebbe quindi alcun bisogno di modalità di calcolo differenti, se non fosse per il fatto che ragionare su espressioni ulteriormente semplificate permette di vedere come influiscono, sui possibili esiti, i diversi parametri in gioco. In questa sede si vuole fornire qualche supporto, anche di tipo grafico, proprio in questa direzione.

Supponiamo allora di trovarci a valle del calcolo, effettuato con i metodi definiti dalle NTC, delle capacità PGA_{C SLV}  e PGA_{C SLV}  e quindi dei periodi di ritorno T_{RC SLV}  e T_{RC SLD.} Disponiamo quindi dei valori delle frequenze  λ_SLV = 1/ T_{RC SLV}  e λ_SLD = 1/ T_{RC SLD}  relative al nostro edificio.

Supponiamo inoltre di utilizzare la possibilità, suggerita dalle Linee Guida, di valutare l_SLC e l_SLO, non mediante il calcolo delle accelerazioni che portano agli stati limite di collasso e di operatività, ma attraverso le espressioni: 

λ_SLC = 0,49 λ_SLV  ;  λ_SLO = 1,67 λ_SLD                                                                                            (2) 

Dopo avere classificato l’edificio in base al suo IS-V, sulla base della tabella delle Linee Guida (riportata, per completezza, in Figura 2a) l’obiettivo adesso è quello di ottenere, basandosi sui due parametri λ_SLV e λ_{SLD ,} il valore dell’indice PAM e classificare quindi l’edificio sulla base della tabella delle Linee Guida riportata in Figura 2b. 

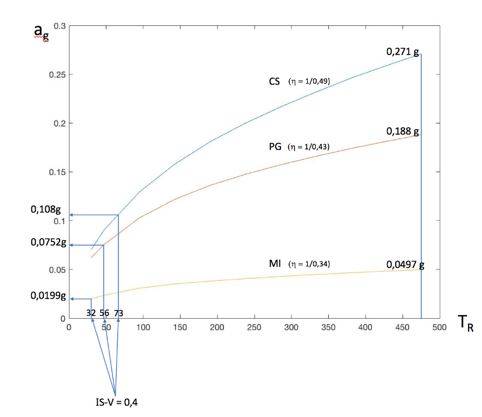
Figura 1. Edifici con lo stesso indice di sicurezza IS-V (nell’esempio: IS-V = 0,4) in zone sismiche diverse hanno periodi di ritorno della PGA_C diversi: maggiori nelle zone a maggiore pericolosità. Le frequenze di ricorrenza, a parità di indice di sicurezza, sono quindi maggiori nelle zone a minore pericolosità. In altri termini: a Milano, il sisma che raggiunge lo SLV per l’edificio con IS-V = 0,4 è più frequente (= ha un periodo di ritorno minore) di quello che riguarda un edificio con lo stesso IS-V a Perugia o a Cosenza. Il risultato potrebbe apparire paradossale (Milano sismicamente più “rischiosa” rispetto a Cosenza?) ma si deve considerare che, proprio per l’ipotesi di avere gli stessi indici di sicurezza IS-V, l’edificio a Milano ha una capacità molto inferiore a quella dell’edificio di Cosenza.

 

Figura 2. Tabelle per la classificazione sismica degli edifici secondo le Linee Guida: a) classe IS-V, b) classe PAM. Vengono qui riportate così come sono nel testo del Decreto, anche se evidentemente sono presenti dei refusi (i casi IS-V>100% e IS-V

Casi possibili e grafico delle classi PAM in funzione delle frequenze

I parametri in gioco sono quindi due, λ_SLV e λ_SLD, ed in funzione di questi valori, seguendo le regole stabilite nelle Linee Guida, si possono avere al massimo otto casi diversi, riassunti schematicamente nella Tabella I, dove sono indicati i rettangoli con i quali si può calcolare l’indice PAM per ciascun caso.

 

Tabella I – Casi possibili: aree sottese e rettangoli con cui si può calcolare l’indice PAM per ciascun caso.

In realtà, i casi 7 e 8 hanno poco interesse, perché, corrispondono a indici PAM comunque maggiori all’8% e la classe sarà quindi sempre la G_PAM. 

Le espressioni delle aree (ovvero l’indice PAM) per ciascun caso si possono facilmente ricavare dalle figure precedenti e sono riportate nella Tabella II.

A titolo di esempio si può vedere come, nel caso 1, si ha: 

PAM = 0,35 λ_SLC + 0,325 λ_SLV + 0,215 λ_SLD + 0,075 λ_SLO + 0,0035 x 0,1 

Utilizzando le (2) e raccogliendo si trova: 

PAM = 0,4965 λ_SLV + 0,34025 λ_SLD + 0,0035

Tabella II – Casi possibili: valori dell’indice PAM in funzione di λ_SLV e λ_SLD.

Le espressioni trovate mostrano come, in molte situazioni (casi 3, 4, 5 e 6) il parametro fondamentale sia λ_SLV, e quindi l’IS-V da cui deriva. Si può vedere in modo ancor più immediato, al di là delle espressioni analitiche di cui sopra, dalla Figura 3, nella quale sono stati riportati, in funzione dei valori di λ_SLV e λ_SLD, le curve di livello dei valori degli indici PAM corrispondenti alle varie coppie λ_SLV, λ_SLD, e quindi i “domini” delle diverse classi.

I valori delle due frequenze sono stati fatti variare tra 0 e 0,1 per λ_SLV (valori maggiori di 0,1 vanno comunque riportati a 0,1 e per questi casi la classe che ne deriva è sempre G_PAM) e tra 0 e 0,14 per λ_SLD.

In realtà, come si nota dal grafico di Figura 3, per valori di λ_SLD > 0,1 le classi variano solo con λ_SLV, rimanendo costante il valore di λ_SLD da assumere (λ_SLD = 0,1).

Come si può notare, il valore di λ_SLD influisce in modo sostanziale sull’indice PAM solo per edifici con valori di λ_SLV bassi (quindi con IS-V relativamente elevati); diventa ininfluente per edifici che hanno indici di sicurezza bassi (come vedremo, per IS-V inferiore a 0,3).

Infatti, se si considera una linea parallela all’asse delle frequenze λ_SLD (Figura 4) e la si fa scorrere idealmente sui diversi valori di λ_SLV ci si accorge che la variabilità dell’indice PAM, e quindi delle classi di rischio, al variare di λ_SLD, è elevata (fino a 5 classi PAM, come già notato in [6]) solo per valori di λ_SLV molto bassi (inferiori a 0,027), per ridursi, in sostanza, ad una sola per λ_SLV > 0,0527.

Rispetto allo SLV, la variabilità delle classi PAM possibili (si consideri, analogamente a quanto fatto prima, una linea parallela all’asse delle frequenze λ_SLV) è invece sempre elevata: da un massimo di otto (= tutto lo spettro di classi possibili) ad un minimo di quattro.

Quanto sopra potrebbe risultare utile per indirizzare gli interventi per i passaggi di classe indicando che in certi casi non è sufficiente “lavorare” sullo SLD (cioè sulla rigidezza) e occorrono incrementi sostanziali dell’indice di sicurezza (innalzando cioè la capacità).

 

Figura 3. Classi PAM in funzione dei parametri λ_SLV e λ_SLD  (il grafico completo è reperibile in [9]).

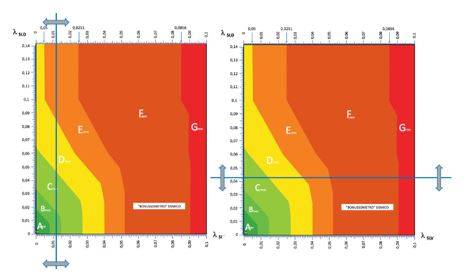
Figura 4. Variabilità del numero di classi PAM al variare di λ_SLV (a sinistra) o di λ_SLD (a destra): pensando di scorrere le due linee sul grafico si può constatare quali siano le zone a maggiore o minore variabilità di numero di classi.

Può essere interessante vedere quali sono i settori del grafico in cui valgono le diverse espressioni di cui alle Tabelle I e II (Figura 5).

 

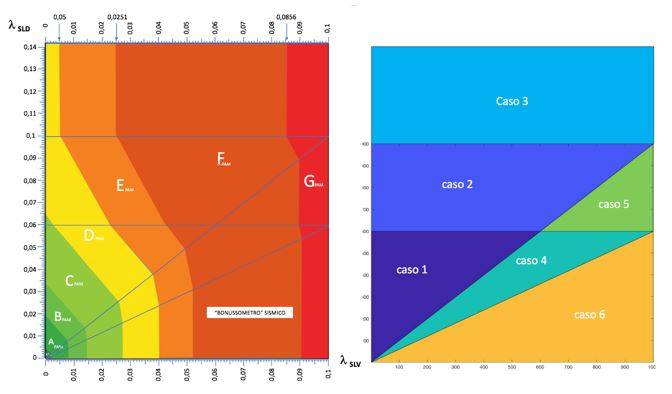
Figura 5. Classi PAM in funzione dei parametri λ_SLV e λ_SLD: zone di validità delle espressioni analitiche dei diversi casi.

Si può qui osservare che nei settori relativi ai casi 3, 5 e 6 la sola variabile in gioco è  λ_SLV e quindi sono utili interventi che riducano tale parametro. In definitiva, i parametri λ_SLV e λ_SLD “giocano ad armi pari” (cioè sono egualmente influenti) solo nei settori dei casi 1 e 2: è qui che si possono ottenere risultati significativi intervenendo sulle rigidezze.  

Influenza del parametro η

La Figura 6a mostra come variano, al variare dell’indice IS-V e per i diversi valori di h, i periodi di ritorno valutati con l’espressione (1) per lo SLV. La Figura 6b mostra una cosa analoga, ma per le frequenze λ_SLV. Le differenze, per valori di IS-V inferiori a 0,4 sono consistenti e possono portare a modifiche significative nelle classi PAM.

Se si considera, ad esempio, un valore di IS-V di poco superiore a 0.3 ci si accorge (Figura 7) delle notevoli differenze di classificazione tra il caso in cui si adotta il valore di η standard (1/0,41) indicato dalle Linee Guida e quello in cui si prende il valore relativo alla zona in cui si trova l’edificio. Ad esempio, a Milano potremmo prendere η = 1/0,34, a Firenze η = 1/0,356, a Perugia η = 1/0,43 e a Cosenza η = 1/0,49. Con quel valore dell’indice di sicurezza, l’edificio che si trova a Milano o a Firenze può essere legittimamente classificato F_PAM invece di D_PAM, mentre per l’edificio con lo stesso indice che si trova a Cosenza oppure a Perugia non cambierebbe alcunché, perché la classe D_IS-V resterebbe comunque la peggiore.

In altri termini, per edifici che hanno valori di IS-V nel range 0,30 - 0,35 e che si trovano nelle zone sismicamente meno pericolose, prendendo il valore di h relativo alla zona invece del valore standard delle Linee Guida si ottiene una classe sismica iniziale due volte peggiore (da D a F) con il “vantaggio” - si fa per dire - di dover fare meno interventi per risalire di due classi. Considerazione analoga si può fare per valori di poco inferiori a 0,3: si potrebbe peggiorare la classe di partenza, passando dalla classe E alla classe G.

 

Figura 6. Variazione dei periodi di ritorno T_{R SLV} (a) e delle frequenze λ_SLV (b) al variare dell’indice di sicurezza IS-V e dei valori di η.

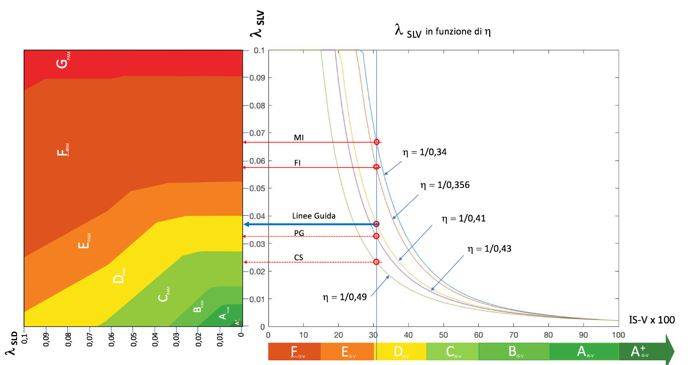
Figura 7. Variazioni di classe PAM, al variare di η, per un edificio con IS-V di poco superiore a 0,3, in città diverse.

Classi PAM in funzione degli indici IS-V e I_{R SLD}

Per una applicazione operativa ancor più immediata, ma soprattutto per osservare come variano le classi PAM con l’indice di sicurezza IS-V e con l’indice di rischio I_{R SLD}, si può considerare il grafico di Figura 8 (riportato, anche in scale diverse, in [9]) , nel quale sono riportati i valori degli indici di sicurezza IS-V e di rischio I_{R SLD} per lo SLD, corrispondenti ai λ_SLV e λ_SLD precedenti, nell’ipotesi di assumere differenti valori di h.

In definitiva, si è passati dalle frequenze λ_SLV e λ_SLD agli indici IS-V e I_{R SLD}  invertendo la (1): 

PGA_C / PGA_D = (T_RD/ T_RC) ^1/η                                                                                                             (3) 

Esaminando le differenze nei valori degli indici sull’asse IS-V, al variare degli η, si può capire quali siano i possibili “margini di manovra” nella classificazione, che per gli edifici in condizioni peggiori nelle zone sismicamente meno pericolose appaiono (forse eccessivamente) ampi. 

 

...CONTINUA LA LETTURA NEL PDF