Ripartizione delle azioni sismiche tra i pali di fondazione con il metodo delle rotazioni congruenti

Nello studio delle fondazioni profonde si ricorre sovente, specie nelle fasi di dimensionamento e di controllo dei risultati numerici, all’utilizzo di modelli semplificati nei quali la fondazione su pali viene analizzata per sottostrutture che si differenziano le une dalle altre in relazione all’azione esterna da ripartire.

Tipici esempi a tal riguardo interessano da un lato la ricerca dell’equilibrio nei confronti dei momenti esterni attraverso sforzi assiali nei pali e dall’altro la suddivisione delle forze orizzontali tra pali incastrati in sommità ad una fondazione che non ruota pur essendo sollecitata dai momenti trasmessi dagli stessi pali.

Il limite di affidabilità dei metodi semplificati consiste nel fatto che le soluzioni per sottostrutture forniscono un quadro parziale in quanto la prima di esse è solamente equilibrata mentre la seconda di esse è solamente congruente, diversamente da quanto accade nei modelli strutturali agli elementi finiti (FEM) in cui le condizioni di equilibrio e di congruenza caratterizzano esplicitamente l’algoritmo risolutivo.

Gli approcci per sottostrutture, se da una parte individuano situazioni limiti di riferimento e di confronto molto utili, dall’altra introducono approssimazioni che possono divenire rilevanti in presenza di azioni orizzontali di notevole intensità come nel caso di azioni sismiche o di venti estremi.

Nel seguito pertanto accanto ad un’ iniziale disamina dei metodi di analisi per sottostrutture si illustra un modello analitico di ripartizione delle azioni esterne tra i pali di una fondazione profonda (fig. 1) che mantenendo la praticità degli approcci semplificati ne supera i limiti imponendo l’equilibrio tra le azioni esterne ed interne nonché la congruenza tra le rotazioni e gli spostamenti dei pali e della fondazione.

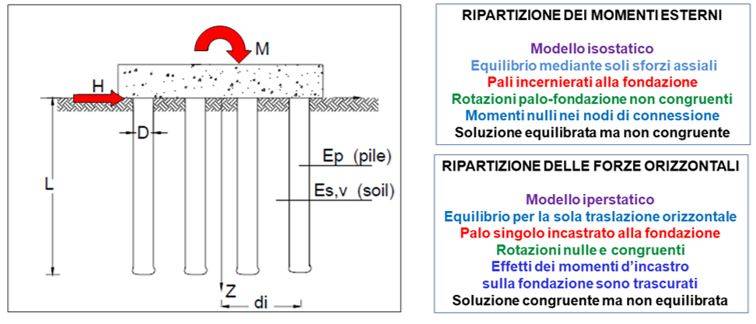
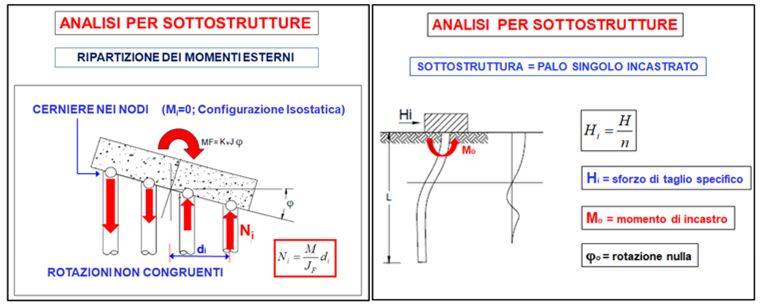
Ripartizione dei momenti esterni

Analisi per sottostrutture - Soluzione equilibrata ma non congruente

La ripartizione dei momenti esterni viene di norma condotta ricercando il valore degli sforzi assiali nei pali eccentrici rispetto all’asse baricentrico che opponendosi ai cedimenti ad essi impressi dalla rotazione della fondazione generano, in virtù della rigidezza verticale del sistema palo-terreno, i momenti antagonisti in grado di equilibrare il momento esterno. Indicata con [φ_F] la rotazione della fondazione e con [d_i] la distanza dell’i-esimo palo dal baricentro della palificata lo spostamento verticale e la reazione assiale risultano valere:

w_i  = φ_F x d_i

Ni = K_v x w_i

La rigidezza verticale [K_v] del sistema palo-terreno si assume eguale per tutti i pali nell’ipotesi che essi abbiano le medesime caratteristiche dimensionali e che l’interazione tra i pali avvenga per il tramite della fondazione come avviene nei modelli strutturali agli elementi finiti in cui il terreno è modellato mediante elementi spring. Eguagliando il momento esterno al momento delle reazioni verticali dei pali si deduce

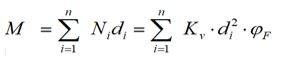
relazione dalla quale, indicata con la notazione:

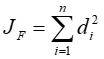
la somma dei quadrati delle distanze dei pali dal baricentro si ricava la rigidezza rotazionale [K_F = M/φ_F]:

K_F = K_V x J_F

e lo sforzo assiale nel palo corrente (fig. 2a):

N_i = (M / J_F) d_i

La distribuzione degli sforzi assiali risulta pertanto, con le ipotesi adottate e fissata l’azione esterna, essere:

• indipendente dalla natura del terreno;
• dipendente dalla sola geometria della fondazione.

Tale circostanza riflette il fatto che la configurazione analizzata è isostatica in quanto corrisponde al modello di pali incernierati in sommità che non scambiano con la fondazione momenti flettenti ma solo sforzi assiali.

Si tratta in altri termini di una soluzione che dipende solo dall’equilibrio rotazionale e che genera distorsioni angolari non congruenti nei nodi.

Questa approssimazione è conservativa nel caso di ripartizione dei momenti esterni, caso in cui i momenti interni di congruenza attivano nei nodi un’azione antagonista che riduce l’azione ribaltante netta agente sulla fondazione. Viceversa tale approccio può rilevarsi inadeguato in presenza di forze orizzontali, caso in cui i momenti di incastro trasmessi dai pali alla fondazione incrementano il momento esterno ribaltante, come mostrato nel seguito.

Ripartizione delle forze orizzontali

Analisi per sottostrutture - Soluzione congruente ma non equilibrata

Il secondo tipo di sottostruttura sovente utilizzata è quella che prende in esame il singolo palo incastrato in sommità (fig. 2b) soggetto alla forza orizzontale specifica (H_i = H / n), caso in cui il regime di sforzi flessionali nei pali dipende dalla legge costitutiva adottata per modellare l’interazione tra palo e terreno. In particolare il momento d’incastro in testa ai pali può esprimersi nella forma unitaria:

M_o = -H_i x h_o

comune sia ai modelli di interazione che schematizzano il terreno mediante il metodo delle reazioni di sottofondo (modelli di Matlock e Reese, Winkler, ecc.) sia come semispazio elastico continuo (modelli di Poulos, Randolph, ecc.). In tale relazione il parametro:

h_o = η_i x L_c 

è una grandezza denominata lunghezza d’inflessione nella quale  η_i è un coefficiente numerico adimensionale dipendente dalla legge costitutiva del terreno mentre L_c è la lunghezza caratteristica del modello di interazione tra palo e terreno (fig. 3).

La soluzione di pali incastrati in sommità soggetti a forze orizzontali dipende da un solo parametro di interazione [ho] e rappresenta un modello congruente in quanto la rotazione dei pali e della fondazione si assumono entrambe nulle, circostanza peraltro verificata solo nel caso limite in cui il sistema palo-terreno abbia una rigidezza verticale infinita in grado di impedire le rotazioni della fondazione che a sua volta é sollecitata, per l’equilibrio dei nodi, dai momenti di incastro trasmessi dai pali. Inoltre essendo nulla per ipotesi la rotazione della fondazione, che trasla rigidamente, sono nulli anche gli spostamenti verticali e di conseguenza anche gli sforzi assiali nei pali.

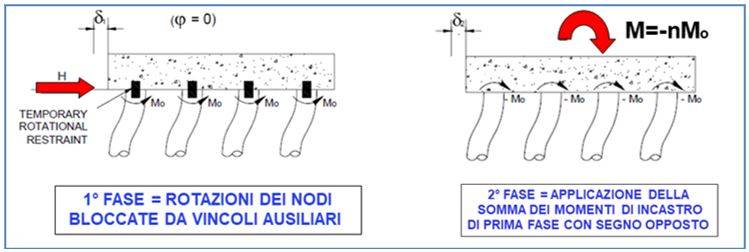
La condizione di pali incastrati in sommità può pertanto essere interpretata come la 1a fase di un procedimento in cui i nodi sono dapprima impediti di ruotare per la presenza di vincoli ausiliari fittizi che vengono poi rimossi in una 2a fase in cui sono consentite le rotazioni ed in cui i momenti di incastro di 1a fase (M_o=-H_i·h_o) sono applicati con segno opposto alla fondazione su pali, che risulta così soggetta ad un momento addizionale pari a (fig. 4):

M^II = H x h_o

...continua la lettura dell'articolo nel PDF.

All'interno anche un caso studio.