Palificate di fondazione soggette a carichi trasversali

Oggetto del presente articolo è l’analisi del comportamento ai carichi trasversali di palificate di fondazione soggette a elevate forze orizzontali (palificate di fondazione per torri e tralicci antisismici, bitte di ancoraggio, strutture di controventamento sismico, ecc.).

Le tipologie di palificate interessate sono quelle con micropali e/o pali di medio e grande diametro verticali e/o inclinati.

I metodi di analisi illustrati consistono nelle analisi semplificate con metodi statici e elastici, per quanto si faranno cenni ai metodi di risoluzione non lineare.

Gli obiettivi della memoria sono illustrare i criteri, le modalità e le fasi di dimensionamento e/o verifica delle palificate soggette a importanti carichi trasversali, con riferimento soprattutto alla determinazione delle risposte del sistema palificata in questa direzione.

Le ipotesi di base

Per l’oggetto e gli obiettivi del presente articolo, non è analizzato il comportamento tenso-deformativo dei pali in gruppo nei confronti dei carichi verticali e dei momenti flettenti (analisi verticale) applicati sull’estradosso della fondazione; infatti il focus della trattazione è imperniato sull’analisi della risposta tenso-deformativa del gruppo di pali nei confronti delle azioni orizzontali (analisi orizzontale) applicate alla struttura di collegamento (che chiameremo platea), ipotizzata infinitamente rigida.

Tale assunzione di platea rigida, largamente accettabile nella maggior parte dei casi, permette di utilizzare metodi di calcolo pragmatici e condivisi, senza necessariamente l’ausilio di softwares specialistici.

Nell’ipotesi di verifica condotta nel solo campo elastico della risposta tenso-deformativa del gruppo di pali, i risultati delle azioni sui singoli pali dedotti dalle differenti analisi (verticale e orizzontale) possono agevolmente comporsi per il principio della sovrapposizione degli effetti (effetti verticali + effetti orizzontali).

Tale assunzione non sarebbe lecita nel caso si esplorasse il comportamento del gruppo nel campo delle deformazioni plastiche; considerate le richieste normative imperniate prevalentemente sulle verifiche allo SLU, si eploreranno soprattutto i metodi agli stati limite sfruttando opportunamente tale principio al fine di disarticolare le analisi a favore di semplicità e di comprensione della meccanica dei sistemi.

Le azioni orizzontali analizzate sono quelle trasmesse alla fondazione dalle sovrastrutture, di natura statica o dinamica (generalmente sismica); pertanto, salvo eventuali momenti indotti dal trasporto dell’azione al piano di interfaccia platea-terreno (momento di trasporto da estradosso a intradosso), le azioni orizzontali considerate sono sempre da intendersi agenti su tale interfaccia; non si analizzerà pertanto il comportamento del gruppo di pali potenzialmente indotto da spostamenti del terreno al di sotto di tale superficie (per esempio da instabilità di versante). Tale argomento è stato ampiamente analizzato dallo scrivente su altre pubblicazioni specialistiche [Froldi, 2011; Froldi et Alii, 2011, Froldi, 2012; Froldi, 2015; Froldi 2020].

Metodi di analisi dei pali in gruppo

Le analisi della risposta tenso-deformativa di un gruppo di pali possono essere sviluppate secondo differenti ipotesi di lavoro, via via più complete e complesse, che dovrebbero, secondo una buona prassi ingegneristica, andare di pari passo con l’approfondimento delle conoscenze del modello geologico e geotecnico locale; non è infatti sensato utilizzare modelli raffinati in assenza di un’adeguata caratterizzazione stratigrafica e meccanica dei terreni di fondazione.

In generale si possono distinguere tre diversi approcci [FHWA, 2018], in progressione dal più semplice al più complesso, ossia metodi basati:

1. sull’equilibrio statico (dalla Statica dei Corpi Rigidi, SCR)
2. su soluzioni elastiche (o delle rigidezze lineari)
3. su soluzioni non lineari (o delle rigidezze non lineari).

In genere tutti i metodi considerano la struttura di collegamento come corpo rigido e il palo (salvo casi particolari) come infinitamente elastico; con tale assunzione, per la regola della SCR possono traslarsi liberamente sulla platea i vettori (sliding vector) forze e trasversalmente anche i vettori momento ortogonali al piano (momento nel piano).

Metodo dell’equilibrio statico

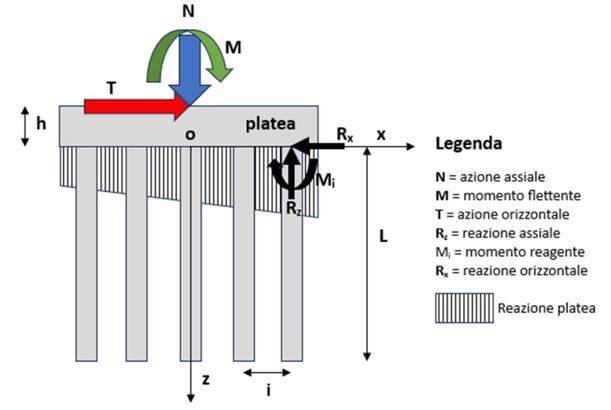
Con il metodo dell’equilibrio statico (SCR) la soluzione di un problema bidimensionale è ricercata attraverso la formulazione delle equazioni di equilibrio delle forze nelle direzioni x, z del piano (la terza dimensioni essendo l’asse y della terna ortogonale orientata) e dei momenti in x,z rispetto a un conveniente punto “o”, che, con riferimento alla successiva figura, in genere si fissa sul centro di simmetria dell’interfaccia platea-terreno:

Σ𝐹𝑥 = 0
                 { Σ𝐹𝑧 = 0 }         [1]
Σ𝑀𝑜 = 0

Le soluzioni delle reazioni verticali (Rz) dei singoli pali possono essere determinate per differenti geometrie (e quindi differenti maglie dispositive e interassi) dei pali, loro lunghezze L e rigidezze assiali, soluzioni che qui si omettono per sintesi.

Le formulazioni che ne scaturiscono (analisi verticale), valide per lo stato di equilibrio limite (SLU), sono espresse in forma esplicita analitica.

In queste stesse soluzioni in genere le azioni di taglio sono ripartite uniformemente sui pali all’interfaccia, trascurando le potenziali differenti rigidezze flessionali e il momento resistente (Mi) che si origina all’innesto del palo nella platea; pertanto le reazioni (Rx), da confrontarsi con quelle allo SLU, saranno uguali per tutti i pali e valgono, per una palificata di n x m pali (analisi orizzontale – solo taglio):

𝑅𝑥 = 𝑇  / (𝑛 ∗ 𝑚)       [2]

Trascurare i momenti resistenti all’innesto dei pali (Mi) nel calcolo di verifica agli SLU, generati dalle reazioni elastiche fornite dalla sezione resistente degli stessi pali, porta a non considerare l’azione flettente globale fittizia (M’) sulla palificata originatisi in corrispondenza degli spostamenti orizzontali, anche in assenza o nel caso di limitatezza delle azioni verticali (N) e di momento (M) trasmesse dalla sovrastruttura all’estradosso della platea (caso di bassi valori di N e M).

Ciò in particolare modo è vero laddove il momento plastico allo SLU della sezione del palo è importante nel comportamento complessivo; in linea di principio e in prima approssimazione, tale semplificazione potrebbe essere accettabile nel caso di micropali, la cui sezione resistente è offerta in genere dalla sola sezione del tubolare d’armatura (MRd di armatura).

Nel caso di reazioni plastiche significative (pali di medio e grosso diametro) è evidente che le precedenti reazioni elastiche dovrebbero essere considerate, in quanto è intuitivo, nonché calcolabile (analisi verticale con solo M), che la struttura di collegamento, sottoposta anche alla sola azione T orizzontale, tenderebbe a ruotare (oltre che per il braccio “h” della T) comprimendo i pali anteriori e traendo quelli posteriori, come schematizzato nella successiva figura (analisi verticale + momento fittizio).

Ovviamente tale soluzione comporta l’ipotesi di assenza di mutue interazioni tra i pali (assenza di effetto gruppo).
In conclusione, se si prescinde dal comportamento tenso-deformativo, ossia non si necessiti di ottenere un diagramma forza orizzontale – spostamento, la verifica agli SLU può essere effettuata con il metodo all’equilibrio statico ricorrendo al principio della sovrapposizione degli effetti sommando opportunamente per ogni palo le reazioni che si ottengono dalle seguenti analisi disaccoppiate:

(analisi verticale) + (analisi verticale + momento fittizio) + (analisi orizzontale – solo taglio)

Il metodo è utilizzabile in quanto, dalla [1] si deduce che la prima equazione lineare (equilibrio lungo x) è indipendente dalle altre due e non viceversa; detta indipendenza vale anche per il sistema delle equazioni lineari posto successivamente in [3], nel metodo delle soluzioni elastiche.

Nel caso di palificata con micropali, l’analisi di sovrapposizione potrebbe essere non particolarmente significativa (per valori di MRd non significativi).

Nonostante il metodo non si utilizza in genere per ottenere una curva carico-spostamento, nell’ipotesi ideale di comportamento di platea e pali di tipo elastico-perfettamente plastico, è sfruttabile anche in tal senso [per il calcolo in campo elasto-plastico dei pali alle forze verticali vedi Froldi, 2023].

...Continua la lettura nel PDF.