MasterSap 2021: l’analisi modale con il metodo dei vettori di carico di Ritz

I prodotti AMV, in particolare quelli legati al software principale MasterSap, modellatore tridimensionale legato all’analisi agli elementi finiti in campo strutturale, sono in continua evoluzione. Oltre al consueto perfezionamento normativo, che ha impegnato gran parte del biennio 2019-20, con gli aggiornamenti alle Norme Tecniche, alla Circolare Applicativa, ai decreti di classificazione sismica ed alle asseverazioni legate al SismaBonus, ci sono anche novità tecnologiche (da ricordare l’evoluzione recente ai sistemi a 64bit) e altre legate a nuove funzionalità. Il 2020 si è chiuso con il rilascio dell’ultima versione di aggiornamento a MasterSap 2020, i cui numerosi contenuti sono illustrati in questi filmati.

Il 2021 si apre con molta altra carne al fuoco, particolare con l’aggiunta di nuovi strumenti e contenuti che renderanno MasterSap sempre più in linea con le richieste professionali legate alla progettazione strutturale.

La verifica sugli edifici esistenti sarà integrata con la gestione degli elementi bidimensionali: solai orizzontali e pareti verticali (nella loro concezione di pareti tozze, estese, oppure snelle, di prevalente sviluppo verticale) potranno essere verificate nell’ambiente di MasterEsist, mentre in ambito BIM vedrà alla luce un plug-in di import/export per la comunicazione con applicativi di modellazione architettonica-strutturale di altre case software.

Per quel che riguarda l’analisi saranno sfruttate le possibilità che dà la progettazione con le regole del comportamento non dissipativo per ottimizzare i dimensionamenti di armature anche nel rispetto della gerarchia delle resistenze, e sarà introdotta una nuova tecnica numerica nel campo dell’analisi modale, che ottimizzerà i tempi di risoluzione delle strutture.

Sintesi del Metodo dei vettori di carico di Ritz per l’analisi modale

È ormai consuetudine per lo strutturista il ricorso agli spettri di risposta per valutare la risposta sismica di strutture di uso civile: tale approccio risulta infatti particolarmente efficiente perché, riferendosi ai valori massimi di (pseudo)accelerazione cui possono essere soggetti oscillatori semplici in funzione del loro periodo di oscillazione, evita di studiare l’intera storia delle accelerazioni trasmesse a terra dal sisma. L’utilizzo degli spettri di risposta richiede dunque la preventiva “decomposizione modale” della struttura, ovvero la trasformazione del sistema originario nella somma “pesata” delle sue forme modali, ognuna dotata di un unico grado di libertà, ottenute attraverso la soluzione di un problema agli autovalori.

Il metodo dei vettori di carico di Ritz si occupa dell’estrazione dei modi propri strutturali (in termini di forme modali e relative frequenze vibrazionali) passando attraverso la trasformazione del sistema discreto originario, ottenuto mediante approccio FEM e quindi generalmente sparso e di grande dimensione, in uno denso e di dimensione molto più ridotta, definito in funzione degli effetti generati dai carichi applicati sulla struttura stessa ed impiegando una opportuna procedura di ortogonalizzazione, quest’ultima volta a definire una base ortonormale del sottospazio nel quale si ambienta il problema ridotto.

Fisicamente, tale trasformazione permette di sintetizzare la distribuzione spaziale della risposta dinamica della struttura in gradi di libertà correlati ai carichi applicati e, poiché il numero di incognite del problema non sarà più pari al numero di gradi di libertà attivi del sistema originario, ma alla dimensione del sottospazio ovvero al numero di vettori della base di Ritz, gli oneri computazionali saranno molto minori, a tutto vantaggio della velocità di soluzione, che potrà inoltre essere calcolata utilizzando i robusti algoritmi dell’algebra lineare per i sistemi densi.

Esempio pratico

Presentiamo di seguito un modello strutturale che risulta esemplificativo dei risultati che si possono ottenere con questa metodologia di calcolo alternativa (metodo dei vettori di carico di Ritz).

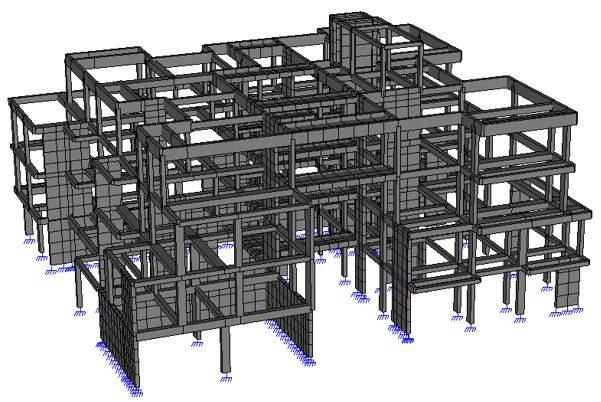
La struttura risulta alquanto articolata ed irregolare, con presenza di numerosi setti, modellati con elementi shell (guscio/piastra) e conta complessivamente 9174 gradi di libertà attivi, che corrisponde alla dimensione del sistema lineare da risolvere.

La trattazione integrale dell'articolo continua nel documento scaricabile in PDF  e stampabile.