La progettazione delle opere di sostegno: come studiare una paratia con modelli rigidi

In alcuni precedenti articoli dello scrivente (Froldi, 2022, Froldi, 2024) si sono trattati i principi che governano la risposta di un palo o un elemento di paratia soggetto a forze orizzontali, siano esse derivanti da opere di sostegno, siano esse derivanti da azioni su fondazioni.

In entrambi i casi le NTC 2018 prescrivono, almeno nella verifica degli SLE e soprattutto laddove possono essere critici gli spostamenti, che siano valutati gli aspetti di interazione tra opera e terreno (cfr. rispettivamente § 6.5.3.2 e 6.4.3.2).

Il presente articolo intende sviluppare riflessioni utili all’analisi dell’interazione di cui sopra nel caso specifico in cui il valore della lunghezza caratteristica o di trasferimento della struttura interagente con il terreno sia contenuta in (struttura infinitamente rigida, vedi Froldi, 2024):

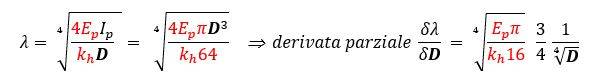
Tale condizione si verifica in pali o paratie molto tozze o in pozzi strutturali di fondazione e la relativa analisi sono ben adatte a tali configurazioni in cui la struttura può essere ipotizzata come soggetta ad una rotazione rigida senza significative inflessioni lungo il proprio asse.

La stessa condizione può verificarsi in corrispondenza di paletti di sostegno di barriere di svio (guardrail) montate su arginelli, in cui la scarsa profondità di infissione a fronte dell’altezza fuori terra e del braccio dell’azione (Es. urto di veicoli con V = 100 kN) rendono quasi certo il fenomeno di rotazione rigida, come rilevato in numerose prove di push-pull sperimentali visionate dallo scrivente.

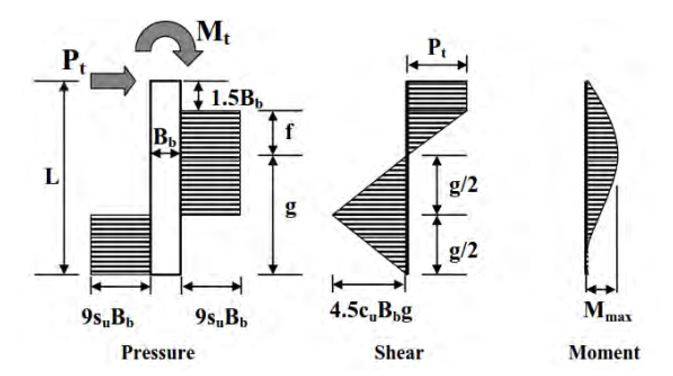
Inoltre tale analisi si presta a sostituire efficacemente il modello agli SLU di Broms (1964, 1965), ormai datato, il quale per le configurazioni dei campi di tensione adotta modelli semplificati e di terreno omogeneo non coerenti con le configurazioni cinematiche prevedibili (vedi Figura 0).

Analisi cinematica piana (in 2D) dell’evoluzione del sistema paratia-terreno – metodo Pressure Based

Con riferimento alla Figura 1, consideriamo un elemento unitario di paratia di pali (o diaframmi in c.a., che chiameremo sinteticamente “paratia”) a presidio di uno scavo alla base di un pendio costituito da una coltre e un substrato, per la quale si conviene che si intendono come agenti le forze agenti (Fa_ext, Fa) da monte a valle (da sx a dx) e come resistenti (Fr) quelle in direzione opposta.

L’ipotesi in studio è che la rigidezza della paratia sia molto grande rispetto a quella del terreno.

Osserviamo che:

• prima dello scavo (FASE -1) la configurazione delle forze agenti sul contatto tra terreno e paratia, a monte e a valle, sarà del tipo come raffigurato in Fig. 1a, ossia caratterizzata da un gradiente nel verso della profondità crescente dato dalla tensione litostatica per l’altezza hm moltiplicata per il coefficiente a riposo del terreno (k0). In questa fase iniziale la velocità del sistema è nulla e il campo vettoriale delle forze è di tipo piano parallelo.
  Piano poiché tutti i vettori forze del campo appartengono al piano.
  Parallelo poiché tutti i vettori forze del campo hanno la stessa direzione.

• dopo lo scavo (FASE 0) la configurazione delle forze agenti sul contatto tra terreno e paratia, a monte e a valle, sarà del tipo come raffigurato in Fig. 1b, ossia caratterizzata da un campo di forze agenti (Fa) parallele al contatto coltre-substrato e da forze resistenti a monte e a valle dell’elemento al di sotto del contatto caratterizzate da un gradiente nel verso della profondità crescente dato dalla tensione litostatica rispettivamente per l’altezza hm e hv moltiplicata per il coefficiente a riposo del terreno. Se si trascurano le componenti verticali del campo di forze agenti (Fa_ext), la configurazione che ne deriva è quella della Fig. 1c, ed è sempre di tipo piano e parallelo.

Mentre la configurazione dei campi di forze in 1c è in equilibrio, quelle dei campi in 1b e 1c non sono più in equilibrio.

Analisi del campo vettoriale piano parallelo

Per chiarezza espositiva formuliamo le seguenti definizioni:

• s_x (z, t) = spostamento orizzontale di un punto della paratia alla coordinata z, al tempo t
• S (Fa_ext ) = campo vettoriale delle forze agenti esterne=costante
• S (Fa) = campo vettoriale delle forze agenti interne=funzione di s(t)
• S (Fr) = campo vettoriale delle forze resistenti (interne)=funzione di s(t)

Atteso che il campo di forze agenti (Fa_ext) al di sopra dello scavo sia costante nel tempo, allora le possibili configurazioni di equilibrio statico dei campi di forza agenti al di sotto dello scavo e resistenti sono potenzialmente infinite e non note a priori; per poter rimuovere le incognite che impediscono la determinazione delle configurazioni possibili, occorre esaminare la cinematica del corpo rigido (paratia) che caratterizza l’evoluzione del sistema paratia-terreno, ossia imporre equazioni di congruenza al sistema.

Per le proprietà della meccanica vettoriale, ogni campo vettoriale piano (nel caso in oggetto si tratta di campi di forze) è equivalente ad un sistema risultante S_R composto o solo da un vettore risultante R o solo da una coppia (o momento) M.

Nella fase di disequilibrio, ossia nelle fasi dinamiche successive alla 0, la risultante (R) dei campi vettoriali paralleli non è nulla, quindi essa si disporrà sull’asse centrale (a) che rappresenta il luogo dei poli rispetto ai quali si annulla il momento vettoriale risultante del campo (M) e costituisce quindi la retta di applicazione del risultante.

Se si considera, come anticipato, la paratia come un corpo infinitamente rigido, anche il suo moto sarà rigido (invarianza delle distanze di tutti i punti del corpo e degli angoli) e il suo atto di moto o campo cinetico (campo vettoriale delle velocità) sarà, al tempo “t”:

• un atto solo rotatorio con vettore velocità di rotazione ortogonale al piano: l’asse di moto si riduce ad un asse di istantanea rotazione normale al piano e il punto C di intersezione dell’asse con il piano della sezione si dice “Centro di Istantanea Rotazione” (CIR)
  
• un atto solo traslatorio in cui tutti i punti hanno la stessa velocità parallela al piano stesso; in questo caso il CIR si pone all’infinito.

Per il teorema di Chasles le normali alle traiettorie dei punti del corpo rigido condotte per le posizioni da essi occupate all’istante “t”, passano tutte per il CIR; tale punto è l’unico della sezione piana su cui giace il corpo che ha velocità nulla all’istante “t” (v_CIR = 0).

Ipotizziamo adesso, con assunzioni semplificative (che verranno illustrate oltre), che le forze resistenti del campo Fr si originino proporzionalmente (per un coefficiente di rigidezza k_x) allo spostamento orizzontale (s_x, piccolo e parallelo a X) in sola compressione del corpo rigido (verso il terreno, alla sua interfaccia, rigidezza lineare in compressione) e senza essere (con trascurabile errore) condizionate dalla sua rotazione. Spostamenti in allontanamento dall’interfaccia considerata non danno luogo a forze resistenti (resistenza alla trazione all’interfaccia nulla, rigidezza in trazione assente).

Si ipotizza, altrettanto ragionevolmente, che la rotazione della paratia non invochi, al suo tergo (lato monte), un campo di forze formato dalle pressioni di spinta attiva al di sopra del CIR; tale assunzione è del tutto realistica allorquando la paratia è formata da pali non contigui, con interasse tale da realizzare un ponte di terreno che si oppone al cedimento plastico del settore di monte. Diversamente, in caso di diaframma continuo in c.a., l’assenza di una spinta attiva a monte si reputa realistica sono in presenza di modesti spostamenti per rotazione della paratia.

...CONTINUA LA LETTURA DELL'ARTICOLO NEL PDF.