L’infinito finito: un ossimoro matematico che svela la complessità del nostro mondo
La matematica sa sorprendere unendo concetti opposti: l’infinito e il finito convivono armoniosamente, rivelando un universo di dettagli nascosti. Tra intervalli numerici senza fine e frattali che riproducono l’infinito in uno spazio finito, scopri come questa meraviglia teorica trova applicazioni nella scienza e nella realtà.
Quando pensiamo all’infinito, immaginiamo qualcosa di inarrivabile, senza confini o limiti. Quando pensiamo al finito, ci riferiamo a ciò che è circoscritto, definito e contenuto.
Ma cosa succede quando uniamo questi due concetti apparentemente opposti?
Nasce l’infinito finito, una realtà che trova applicazione non solo nella matematica teorica, ma anche nel mondo reale.
Che cosa è l’infinito finito?
L’infinito finito è un concetto che racchiude l'idea di infinito all'interno di un limite apparente o reale. Non è una contraddizione, ma una combinazione di concetti che convivono grazie alla logica matematica.
Ad esempio:
- Un insieme infinito ma limitato è uno spazio contenente infiniti elementi che, tuttavia, si trovano all'interno di un confine ben definito.
- Una somma infinita può produrre un risultato finito, quando i termini della somma decrescono abbastanza rapidamente.
L’infinito finito è dunque una "finestra" sull’infinito, visibile all'interno di limiti ben precisi.
Esempi di infinito finito
L'intervallo [0,1]
L’intervallo numerico tra 0 e 1 contiene infiniti numeri, eppure è limitato alle estremità da 0 e 1.
Ad esempio, i numeri 1/2, 1/3, 1/4 ... e così via formano una successione infinita, ma restano confinati all'interno di questo intervallo.
Serie infinita convergente
Consideriamo la somma infinita:
S = 1 + 1/2 + 1/4 + 1/8 ... = 2
Sebbene la serie contenga infiniti termini, il totale della somma si avvicina sempre di più a 2 senza mai superarlo. Questo è un esempio di come un infinito (i termini della serie) possa risultare in qualcosa di finito (il valore della somma).
La lunghezza della linea di Koch:
La curva di Koch è una figura geometrica frattale. A ogni iterazione, si aggiungono segmenti sempre più piccoli, rendendo la lunghezza totale teoricamente infinita, ma la curva rimane confinata in uno spazio finito.
La linea di Koch
La linea di Koch, nota anche come curva di Koch o fiocco di neve di Koch, è un famoso esempio di frattale, una figura geometrica che presenta un’infinita complessità pur essendo contenuta in uno spazio finito. Ideata dal matematico svedese Helge von Koch nel 1904, si costruisce iterativamente: si parte da un segmento e, a ogni passaggio, si divide in tre parti uguali, sostituendo la parte centrale con due lati di un triangolo equilatero. Questo processo, ripetuto all’infinito, genera una curva che ha lunghezza infinita ma occupa un'area finita. La linea di Koch illustra la bellezza e il paradosso dei frattali.
Spiegazione matematica approfondita
Serie infinite convergenti
Per comprendere il concetto di infinito finito, analizziamo una serie infinita convergente.
Una serie è definita come la somma dei termini di una successione:
S = α1 + α2 + α3 +…
Se i termini della serie αn decrescono abbastanza rapidamente, la somma S si avvicina a un valore finito.
Ad esempio, nella serie geometrica:
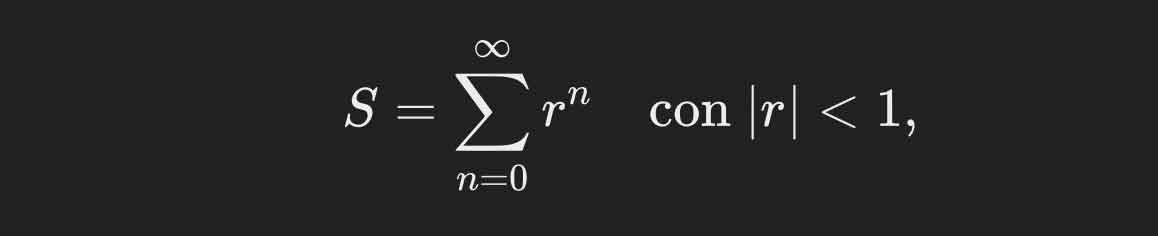
si dimostra che:
S = 1/(1-r)
Questa formula ci dice che, pur avendo infiniti termini, la somma totale è un numero finito.
Insiemi infiniti limitati
Un insieme come [0, 1] contiene infiniti numeri reali.
Questo è dovuto alla proprietà dei numeri reali: tra due numeri qualsiasi esiste sempre un altro numero.
Tuttavia, l'insieme è "finito" in termini di estensione, poiché è limitato da 0 e 1.

Usi dell’infinito finito nel mondo reale
-
Tecnologia digitale:
Nei computer, le immagini e i video sono rappresentazioni finite, ma costruite su basi infinite. Ad esempio, un'immagine digitale è un insieme finito di pixel che può avvicinarsi all’infinitamente dettagliato aumentando la risoluzione. -
Finanza e economia:
I concetti di serie infinite sono usati nei modelli di investimento e nei calcoli di interessi composti. Per esempio, il valore attuale di un flusso infinito di pagamenti futuri può essere calcolato come una somma finita usando le formule delle serie geometriche. -
Fisica:
I frattali, che rappresentano strutture infinite ma limitate, sono utilizzati per descrivere fenomeni naturali come la struttura dei polmoni, il letto di un fiume o le coste.
Curiosità finali sull’infinito finito
Il Paradosso di Zenone:
Zenone di Elea propose un paradosso in cui Achille non può mai raggiungere una tartaruga che parte in vantaggio. Questo è un esempio filosofico di infinito finito: l’infinità di passi può essere sommata in un tempo finito.
I frattali nella natura:
Molte strutture naturali seguono modelli frattali: una quantità infinita di dettagli si manifesta in uno spazio finito. Ad esempio, un albero può avere infiniti rami sempre più piccoli, ma resta contenuto entro la sua altezza.
Arte e infinito:
L'artista Maurits Cornelis Escher ha spesso esplorato l'infinito finito nelle sue opere, come nei disegni di scale o di figure che si ripetono all'infinito entro spazi limitati.
Conclusione
Il concetto di infinito finito racchiude una tensione filosofica profonda, che ha affascinato pensatori di epoche diverse.
Esso rappresenta la possibilità che l’infinito, tradizionalmente associato a ciò che è illimitato e inconcepibile, si manifesti in forme limitate e comprensibili.
Questa idea ha avuto implicazioni significative nel pensiero metafisico e matematico.
Aristotele fu tra i primi a distinguere tra infinito potenziale e infinito attuale. Per lui, l'infinito potenziale è qualcosa che può essere sempre superato, come il processo di suddivisione di un segmento; l'infinito attuale, invece, è il completamento di tale processo, una realtà che Aristotele negava nel mondo fisico. Questa distinzione riflette la dualità del concetto di infinito finito.
Nel XVIII secolo, Georg Cantor, il fondatore della teoria degli insiemi, rivoluzionò la matematica dimostrando che esistono infiniti diversi, alcuni dei quali “contenibili” in sistemi strutturati come i numeri reali. La sua opera fu anche oggetto di critiche teologiche, poiché mostrava come l’infinito potesse essere trattato matematicamente, sfidando l’idea di infinito come attributo esclusivo di Dio.
Più recentemente, David Bohm, fisico e filosofo, ha esplorato l’infinito finito nella struttura dell’universo, suggerendo che l’intero possa essere riflesso nelle sue parti, in una relazione tra finito e infinito che ricorda i frattali.
Questa dialettica stimola il pensiero filosofico, suggerendo che i limiti del nostro mondo possano contenere un riflesso dell’eternità.
Esso non solo arricchisce la nostra comprensione del mondo, ma si rivela anche uno strumento pratico per la scienza, la tecnologia e persino l’arte. Forse, in fondo, è proprio questa sintesi di opposti a rendere la matematica così profondamente affascinante.
Matematica
Condividi su: Facebook LinkedIn Twitter WhatsApp

