Impalcati da ponte: studio con metodi energetici di sezioni multicellulari soggette a torsione

Gli impalcati con sezioni di forma multicellulare trovano da tempo largo impiego nei ponti stradali e ferroviari ed in costruzioni affini essendo caratterizzati da elevate rigidezze torsionali che consentono di attivare un’efficace ripartizione dei carichi mobili e delle altre forze esterne [1],[2].

Lo studio di queste tipologie strutturali risulta in genere complesso e viene oggi affrontato utilizzando di prassi modelli e software agli elementi finiti di grande efficacia, versatilità ed accuratezza computazionali.

Tuttavia i metodi numerici non rendono direttamente palesi le cause dell’articolata interazione che si instaura tra le varie celle nel fronteggiare e ripartire il momento torcente esterno né dei contributi forniti dalle singole celle alla rigidezza torsionale complessiva.

Per ovviare a questa limitazione si possono impiegare in sinergia con i metodi numerici i metodi analitici che ben si prestano, specie nei casi di geometria regolare, ad identificare i parametri torsionali adimensionali che caratterizzano le sezioni multicellulari, come descritto nella memoria.

Finalità dello studio: determinare la rigidezza torsionale primaria

Nel contesto delineato lo studio si pone l’obiettivo di determinare la rigidezza torsionale primaria di una sezione a celle multiple (fig. 1a) estendendo a tale caso il criterio energetico utilizzato da Bredt per le sezioni chiuse a cella singola.

Tale criterio può essere impiegato anche nel caso delle sezioni pluriconnesse avendo l’avvertenza di sommare al lavoro di deformazione diretto il lavoro di deformazione mutuo compiuto dalle tensioni e dagli scorrimenti tangenziali afferenti a celle attigue, contributo invece necessariamente assente nella soluzione di Bredt.

Questo aspetto ben si coglie confrontando le rigidezze torsionali ottenute mediante metodi analitici con quelli relative a situazioni limite di più semplice e diretta valutazione, utili anche ai fini interpretativi. Tali configurazioni limite si identificano da un lato con la somma diretta delle rigidezze torsionali delle singole celle e dall’altro lato con la somma delle rigidezze torsionali delle sezioni chiuse contenute le une nell’altre in cui può pensarsi scomponibile la sezione pluriconnessa (fig. 1b).

Si può mostrare infatti che le rigidezze torsionali effettive delle sezioni multicellulari regolari risultano comprese tra i valori pertinenti alle due situazioni limite citate, circostanza che si spiega mettendo in conto il lavoro di deformazione reciproco compiuto dai flussi tensionali elementari afferenti alle singole celle chiuse in cui il flusso tensionale complessivo può essere scomposto.

Tali flussi elementari esplicano la propria azione mutua lungo i tratti delle celle in cui esse si sovrappongono garantendo attraverso il lavoro reciproco la congruenza delle rotazioni torsionali e dei movimenti.

Nella prima situazione limite di singole celle indipendenti il lavoro mutuo dei flussi elementari ha segno negativo e contrasta il lavoro diretto fornendo un contributo irrigidente che consente di ricomporre la indeformabilità del contorno della sezione che le singole celle non interagenti violano.

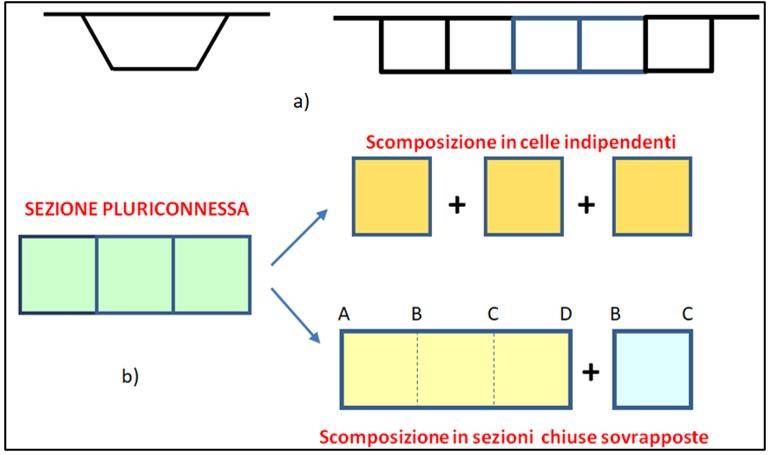
Nella seconda situazione limite di sezioni chiuse inglobate le une nelle altre il lavoro di deformazione mutuo è invece positivo e si aggiunge al lavoro diretto riducendo la rigidezza complessiva delle sezioni chiuse non interagenti.

La legge quadratica che esprime il lavoro di deformazione interno in funzione delle tensioni tangenziali non permette infatti di operare la semplice addizione dei lavori interni diretti né di conseguenza la somma delle proprietà inerziali delle singole celle. Occorre pertanto riferirsi ad un modello teorico di validità generale.

Sezioni chiuse

Come approccio introduttivo utile per il prosieguo si richiama la statica delle sezioni a cella singola. Il regime tensionale di una sezione chiusa monocellulare è descritto dalla soluzione di Bredt che per le tensioni tangenziali lungo il perimetro della sezione chiusa fornisce la relazione:

τ = M_t / 2 Ω s

 
nella quale [Mt] è il momento torcente esterno, [Ω] è l’area racchiusa dalla linea media del contorno della sezione mentre [s] è lo spessore locale della parete sottile. Per quanto concerne invece le deformazioni torsionali la rotazione unitaria [θ=dθ/dx] indotta dall’azione torcente si ricava imponendo l’eguaglianza del lavoro esterno e del lavoro interno ottenendo la relazione:

θ = M_t / GJ_t

in cui G è il modulo elastico tangenziale del materiale mentre J_t è il momento d’inerzia torsionale:

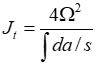
Sezioni multicellulari

Lo studio delle sezioni chiuse multicellulari risulta più articolato dovendosi determinare più flussi tensionali incogniti [τ_i=τ_is_i] che si sviluppano lungo i vari rami della sezione e la rotazione torsionale unitaria.

Una generalizzazione diretta della formula di Bredt per le sezioni pluriconnesse non è ottenibile in forma chiusa ma è possibile pervenire ad una soluzione rigorosa nell’ambito dell’ipotesi di sezione a contorno indeformabile e di materiale elastico.

A tal riguardo occorre tenere presente che le tensioni tangenziali devono attingere valori tali da soddisfare l’equilibrio alla traslazione longitudinale in corrispondenza dei nodi, la congruenza delle rotazioni torsionali unitarie delle celle e l’equilibrio rotazionale della sezione (Belluzzi [3]). Tali requisiti si esplicitano da un punto di vista applicativo in condizioni inerenti:

1. la continuità del flusso tensionale nei nodi;
2. la circuitazione del flusso delle tensioni tangenziali all’interno delle singole celle;
3. l’eguaglianza tra il momento torcente esterno ed il momento dei flussi tangenziali.

...CONTINUA LA LETTURA NEL PDF