Identificazione dinamica di una torre piezometrica

Spesso le torri piezometriche hanno valenza storica, è importante sottoporle a controlli senza generare impatti visivi o strutturali

In Italia sono presenti un gran numero di Torri Piezometriche, strutture che, se attive, oltre ad avere un’importanza strategica in quanto garantiscono la fornitura d’acqua a un consistente bacino d’utenza, hanno nella maggior parte dei casi, per la loro imponenza, un impatto paesaggistico di grande rilevanza. Considerato il fatto che molto spesso hanno anche valenza storica, ecco l’importanza e la necessità di doverle sottoporre a controlli tali da non generare su di esse impatti visivi e strutturali.
In questi casi è la tecnologia e le innovazioni ad essa legata che supportano e risolvono problematiche di vario tipo, legate soprattutto a controlli distruttivi e impattanti sulle strutture.
Tra tali tecnologie per il controllo strutturale, hanno un ruolo principe i monitoraggi automatici in continua ad acquisizione da remoto che, oltre ad avere un impatto molto ridotto sui manufatti, garantiscono risposte chiare, affidabili ed efficaci.

Il presente articolo, avente come argomento principale l’identificazione dinamica di una torre piezometrica, ovvero l’individuazione delle frequenze fondamentali d’oscillazione, rappresenta la seconda pubblicazione relativa all’attività di monitoraggio di un manufatto di questo tipo. È stata condotta per mezzo dell’elaborazione dei dati accelerometrici acquisiti nel corso del monitoraggio, per poi procedere ad un confronto con quanto ottenuto approssimando il suo comportamento a quello di un sistema SDOF (Single Degree of Freedom System).
L’intera esposizione è un estratto della tesi di Laurea Magistrale in Ingegneria Civile dell’Ingegnere Antonio Mucciarone, sviluppata durante l’esperienza di tirocinio svolta presso la società IndaginiStrutturalisrl.

Sistema dinamico ad un grado di libertà

Nel presente capitolo verranno riportati i concetti base che definiscono la dinamica di un sistema a 1 grado di libertà, fondamentale per la successiva identificazione dinamica analitica della torre, a seguito di una sua approssimazione ad un sistema SDOF (Single Degree of Freedom).

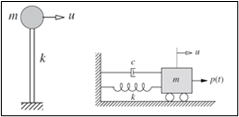
Per l’individuazione delle frequenze naturali bisogna far riferimento alle condizioni di vibrazione libera, ovvero di un sistema che viene disturbato dalla sua condizione di equilibrio statico e lasciato vibrare senza l’applicazione di alcuna sollecitazione esterna e smorzamento.

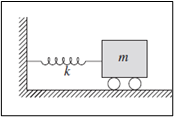
Il moto di un sistema avente tali caratteristiche viene descritto dall’equazione differenziale mu ̈+ku=0 , dove m e k rappresentano rispettivamente la massa [kg] e la rigidezza [N/m] del sistema.
Per consentire la realizzazione delle vibrazioni libere, è necessario procedere nello spostare la massa dalla sua condizione di equilibrio statico, imponendo uno spostamento iniziale u(0) e/o una velocità iniziale u ̇(0).
Essendo l’equazione del moto del suddetto sistema un’equazione differenziale omogenea del secondo ordine a coefficienti costanti, è nota la forma della sua soluzione, potendo così definire l’equazione dello spostamento del sistema come u(t)=u(0) cos⁡〖ω_n t〗+(u ̇(0))/ω_n sin⁡〖ω_n t〗, dove ω_n rappresenta la pulsazione naturale del sistema ricercata e così definita:

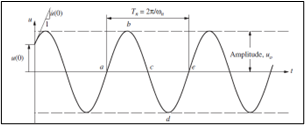
Dall’andamento temporale delle oscillazioni di un tale sistema, è possibile constatare come queste avvengano a frequenza ω_n e ad ampiezza costante
Però, tutte le strutture sono caratterizzate inevitabilmente dalla presenza di uno smorzamento, il quale racchiude gli effetti che comportano la dissipazione di energia, tale da condurre ad una diminuzione delle ampiezze delle oscillazioni naturali nel tempo fino ad annullarle del tutto, oltre ad una modifica delle frequenze con cui queste avvengono (trattasi sempre di oscillazioni naturali se nulle le sollecitazioni esterne).
Si vuole però evidenziare come le strutture siano caratterizzate da bassi valori di smorzamento, i quali conducono ad una riduzione delle ampiezze delle oscillazioni nel tempo ma caratterizzate da un valore di frequenza pressoché identico a quello di un sistema non smorzato.

Confrontando gli andamenti delle oscillazioni non smorzate e sottosmorzate (come per il caso tipico delle strutture) di due sistemi dotati della medesima massa e rigidezza, risulta facilmente individuabile come i loro valori di picco vengano registrati nel medesimo istante temporale, comprovando come in tali condizioni le frequenze dei sistemi siano pressoché analoghe.

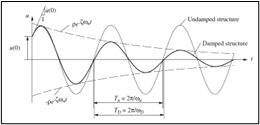
Quest’ultima considerazione consente di poter stabilire come sia possibile procedere ad una idealizzazione della torre ad un sistema SDOF non smorzato, al fine di identificare la sua pulsazione naturale mediante considerazioni di natura puramente analitica.

Identificazione dinamica sperimentale

La caratterizzazione dinamica di una struttura consiste nel descrivere il suo comportamento dinamico come una combinazione di modi di vibrare, ognuno caratterizzato da una frequenza naturale di oscillazione, coefficiente di smorzamento e forma modale. I parametri modali sono da interpretarsi come l’impronta digitale della struttura, le quali sono esclusivamente funzione delle sue caratteristiche intrinseche (ad esempio massa, proprietà meccaniche dei materiali, rigidezza elementi strutturali, condizioni di vincolo).

Questo significa che eventuali modifiche subite dalla struttura possono essere individuate anche osservando variazioni significative delle caratteristiche dinamiche. Pertanto, l’identificazione dinamica può essere introdotta in diversi campi di applicazione come, ad esempio, la taratura di modelli FEM di strutture già esistenti, lo svolgimento di campagne di monitoraggio strutturale per stabilire il reale stato di conservazione della struttura (Structural Health Monitoring – SHM), oppure la valutazione dell’efficacia di interventi di consolidamento.

L’importanza dell’analisi dinamica è connessa alla possibilità di valutare gli effetti che i carichi dinamici potranno produrre sulla struttura stessa, confrontando le caratteristiche di entrambe. Infatti, le condizioni più pericolose si verrebbero a generare quando il contenuto in frequenza della sollecitazione agente contiene al suo interno le frequenze proprie della struttura, provocando il cosiddetto fenomeno della risonanza, con un conseguente incremento dell’ampiezza delle oscillazioni ed il rischio di giungere alla formazione di danni strutturali rilevanti.

L'ARTICOLO CONTINUA...