Effetti dei movimenti tettonici nei ponti sospesi di grande luce

Negli ultimi secoli il volume di traffico via mare è aumentato notevolmente e sta tuttora aumentando e, con esso, anche le dimensioni delle imbarcazioni. Ciò rende necessario allargare lo spazio libero per la navigazione e, di conseguenza, realizzare ponti di luce sempre maggiore.

La soluzione di luci maggiori su un numero minore di pile è anche notoriamente meno costosa rispetto a quella di luci minori su un numero maggiore di pile, specie se con fondazioni profonde in acqua. Anche il vantaggio di ridurre il rischio di collisione di natanti contro i piloni non va trascurato.

Attualmente il primato della luce spetta al 1915 Canakkale Bridge, sullo stretto dei Dardanelli in Turchia, aperto al traffico nel 2022: la sua campata centrale raggiunge i 2023 m.

Com’è noto, nel recente passato sono stati proposti diversi ponti di luce maggiore: tra questi il ponte sullo stretto di Messina, il cui progetto prevede una campata centrale di 3300 m, e quello sullo stretto di Gibilterra, per il quale esistono due proposte, una con luci di 3500 m e una con luci di 5000 m.

Tali distanze sono attualmente superabili con campate sospese a funi di acciaio armonico (Pugsley 1968, Buonopane and Billington 1993, Clemente 2022).

La notevole distanza tra i punti di ancoraggio al suolo pone per tali ponti un problema che normalmente non si pone per strutture di dimensioni ordinarie: la possibilità di spostamenti tettonici tra le fondazioni e la variabilità spaziale dell’input sismico (Antonioli et al. 2002, Barreca et al. 2021, Doglioni et al. 2012, Lo Presti et al. 2022).

Spesso un ponte sospeso supera una o più faglie (Jia et al., 2012); è probabile, quindi, che possa essere interessato da movimenti tettonici lenti ma anche da violenti terremoti.

Accadde in Giappone il 15 gennaio 1995, quando un violento sisma colpì l’Akashi Kaikyo Bridge, allora in costruzione, causando uno spostamento residuo di circa 1 m di uno dei due piloni (Yamagata et al., 1996). L’impalcato fu ridisegnato, adattandolo alla nuova geometria, e la costruzione proseguì. Al momento dell’inaugurazione nel 1998, l'Akashi Kaikyo era il ponte più lungo al mondo e ha tenuto il primato fino al 2022.

Schema tipico di un ponte sospeso

Lo schema tipico di ponte sospeso prevede una campata centrale di lunghezza L e due campate di riva, di lunghezze rispettivamente L_a e L_b (Figura 1).

In quella centrale, l’impalcato è in genere sospeso a due funi parallele, poste alle estremità trasversali dell’impalcato stesso, tramite pendini; in quelle laterali, l’impalcato può essere sospeso per tutta la lunghezza delle funi o per solo una parte di esse o non essere sospeso bensì sostenuto da pile o altre strutture indipendenti.

Le campate laterali possono anche non rispettare la simmetria, presentando luci diverse, come diverse possono essere le lunghezze delle porzioni di impalcato sospese.

Le funi sono rigidamente ancorate al suolo alle loro estremità (A e D), mentre possono scorrere in sommità ai piloni (B e C) evitando di trasmettere a questi il tiro, ossia la componente orizzontale dello sforzo nelle funi stesse.

A volte le estremità delle funi si chiudono sull’impalcato, trasmettendo ad esso un notevole sforzo di compressione: si parla, in tal caso, di sistema auto-ancorato, che non viene utilizzato per ponti di grande luce.

Il comportamento di un ponte sospeso è influenzato anche dal contributo irrigidente della travata che, però, si riduce al crescere della luce fino a diventare pressoché ininfluente per ponti di grandissima luce.

Nel seguito si farà riferimento allo schema con le tre campate interamente sospese alle due funi. Pertanto, anche il carico permanente w sarà pressoché uguale nelle tre campate. Inoltre, si assumeranno i seguenti rapporti tipici tra le varie grandezze geometriche:

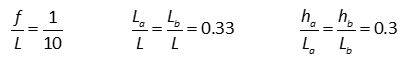
La luce limite di un ponte sospeso 

Quale è la luce massima realizzabile con lo schema sospeso e con i materiali attualmente disponibili?

Si consideri il caso di una fune soggetta soltanto al suo peso proprio. Con riferimento a ponti di grande luce, il rapporto f/L assume valori non superiori a 1/10 e, pertanto, il peso proprio della fune w_c può essere approssimato a un carico uniformemente distribuito:

 w_c = γ_c A_c x (l/L) = γ A_c 

essendo la lunghezza della fune nella configurazione deformata sotto il suo peso proprio. Il peso specifico γ è, quindi, un peso specifico equivalente che tiene conto dell’effettiva lunghezza della fune ed è proporzionale a  γ_c . In presenza del solo peso proprio della fune, il tiro vale:

H = γ A_c x (L / (8f / L)

e lo sforzo massimo (in B e C) è:

N_max =  γ A_c x (L / (8f / L cos α)

Essendo α l’angolo che la tangente alla fune forma con l’orizzontale. Eguagliando N_max allo sforzo di progetto del cavo, pari a f_d A_c, con f_d tensione di calcolo e A_c area del cavo, si ottiene il massimo valore della luce, che dipende soltanto dalle caratteristiche del materiale e dalla geometria della struttura ma non dall’area del cavo: 

Con f/L cosα ≈ 0.1 e assumendo valori usuali per il peso specifico e la resistenza dell’acciaio armonico (f_d/γ ≈ 10⁴ m), risulta L_lim ≈ 8000 m.

Si può dimostrare (Clemente et al., 2000) che, detto β il rapporto tra il carico addizionale (sovraccarico permanente + carico mobile, entrambi uniformemente distribuiti sull’intera luce) e il peso proprio, per ciascuna fune, tiro e sforzo massimo diventano, rispettivamente:

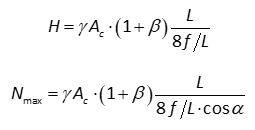
e la luce limite risulta:

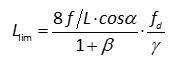
Per  = 1, ossia nel caso di fune in grado di portare un carico addizionale pari al peso proprio, la luce limite si dimezza, risultando pari a circa 4000 m. La possibilità di realizzare ponti di luce maggiore, come ben noto, è legata al rapporto e, quindi, alla disponibilità di materiali più resistenti e più leggeri.
La configurazione meccanica e geometrica della struttura in presenza dei soli carichi permanenti, nell’ipotesi usuale di piloni alla stessa quota, può essere rappresentata tramite il parametro adimensionale

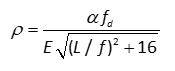
dove α (<1) rappresenta il rapporto tra la tensione in presenza dei soli carichi permanenti (peso proprio delle funi + sovraccarichi permanenti) e la tensione di calcolo f_d. Nel seguito si assumerà α = 0.9, valore tipico per ponti di grande luce.

,,,continua la lettura dell'articolo nel PDF.

L'articolo continua con la trattazione degli effetti di uno spostamento relativo tra i piloni,