Analisi non lineare di sottovie in c.a. su suolo elastico mediante un approccio FE-BIE
Nella memoria l'interazione
suolo-struttura viene analizzata per mezzo di un approccio misto FE-BIE.
La struttura è modellata con elementi beam in spostamenti, mentre l'interfaccia fra struttura e substrato è descritta in termini di stato tensionale facendo uso di un'equazione integrale al contorno basata su di un'opportuna funzione di Green.
Le non linearità del materiale vengono riprodotte mediante un approccio a plasticità concentrata definendo, alle estremità degli elementi beam, connessioni semirigide con legame momento-rotazione di tipo rigido-plastico. Le analisi incrementali condotte evidenziano l'efficacia del modello nel cogliere meccanismo di collasso e progressiva perdita di rigidezza della struttura sotto carichi crescenti.
Nonlinear analysis of RC tunnels on elastic soil using a FE-BIE approach
Analisi non lineare di sottovie in c.a. su suolo elastico mediante un approccio FE-BIE
D. Baraldi1, F. Minghini2, E. Tezzon2, N. Tullini2
- 1 Department of Architecture, Construction and Conservation, University IUAV of Venice, Venice, Italy
- 2 Department of Engineering, University of Ferrara, Ferrara, Italy
Introduzione
La valutazione dell'interazione suolo-struttura rappresenta da tempo una sfida per l'ingegneria strutturale.
Le soluzioni analitiche al problema sono ristrette ai casi dell'indentatore rigido e della trave di lunghezza infinita su semispazio elastico, isotropo o anisotropo (Johnson 1985, Kachanov et al. 2003).
Negli altri casi si fa uso, generalmente, di semplici modelli di suolo, come quelli di Winkler e Pasternak (Selvadurai 1979).
Tali modelli, tuttavia, sono appropriati purché si possano trascurare gli effetti dovuti all'interazione trasversale fra parti adiacenti della superficie del substrato.
Riguardo ai modelli numerici, l'interazione suolostruttura è stata analizzata in passato mediante vari approcci.
In uno di questi (Selvadurai 1979) si fa uso del metodo degli elementi finiti (FEM) per discretizzare sia la fondazione sia il substrato. Tale approccio, pur consentendo di descrivere geometrie complesse, comporta spesso un eccessivo onere computazionale, in quanto la mesh del substrato deve essere estesa ben oltre i confini della superficie caricata per garantire, lontano dai carichi, le condizioni di suolo indisturbato. Per migliorare l'efficienza numerica sono stati proposti elementi infiniti (Wang et al. 2005). In ogni caso, l'uso di elementi beam per la fondazione e di elementi bidimensionali per il suolo comporta la perdita della continuità delle rotazioni all'interfaccia.
Le prime applicazioni di modelli di semispazio elastico si devono a Cheung e Zienkiewicz (1965) e Cheung e Nag (1968). Tali formulazioni fanno uso della soluzione di Boussinesq ed introducono collegamenti equispaziati fra la fondazione ed il substrato mediante link rigidi con vincoli di incastro ad un estremo e cerniera all'altro. Pertanto, non è consentito imporre la continuità delle rotazioni all'interfaccia.
Inoltre i modelli citati richiedono l'inversione esplicita della matrice di flessibilità del substrato. Kikuchi (1980) ha introdotto per la prima volta una formulazione variazionale che include un'opportuna funzione di Green per il suolo. Bielak e Stephan (1983) hanno studiato la flessione di travi su suolo elastico usando una funzione di Green derivata dalla funzione di influenza di Boussinesq.
Uno strumento particolarmente vantaggioso per l'analisi di semispazi elastici è rappresentato dal Boundary Element Method (BEM), che consente di discretizzare solo l'interfaccia con la sovrastruttura (Ribeiro & Paiva 2015)....
Tuttavia, le reazioni del suolo vengono tipicamente considerate come reazione ni nodali nel modello agli elementi finiti della sovrastruttura e quindi, anche in questo caso, si perde la continuità delle rotazioni all'interfaccia.
In questa nota vengono presentate analisi in stato piano di strutture poggianti su semispazio bidimensionale omogeneo, elastico lineare e isotropo, condotte mediante un modello misto FE-BIE. Il modello si basa su una formulazione numerica in spostamenti per la struttura (FE), combinata con un'equazione integrale per l'interfaccia fra suolo e struttura (BIE).
Le variabili indipendenti del modello sono spostamenti e rotazioni nodali della struttura e tensioni normali e tangenziali all'interfaccia. Un modello analogo è stato usato da Tullini e Tralli (2010) e Tullini et al. (2012, 2013a, b). Diversamente da altri modelli disponibili in letteratura, tale formulazione impone la continuità delle rotazioni nei nodi comuni fra struttura e substrato; inoltre conduce ad una matrice simmetrica per il substrato, permettendo così di evitare gli inconvenienti legati alla non simmetria della matrice dei coefficienti del BEM.
Infine, la matrice risolvente del modello ha dimensioni proporzionali al numero di elementi finiti della fondazione.
Al contrario, nel FEM un raffittimento della mesh conduce ad una matrice di rigidezza di dimensioni pari a diverse volte il quadrato del numero di elementi usati per la fondazione. In definitiva, il modello misto utilizzato consente di ottenere soluzioni accurate con un costo computazionale inferiore.
Per tenere conto della non linearità del materiale, è stata implementata una formulazione a plasticità concentrata modificando il metodo proposto da Hasan et al. (2002) per incorporare il modello di connessione semirigida di Shakourzadeh et al. (1999).
Tale modello, che interviene sulla matrice dell'elemento nel riferimento locale senza prevedere gradi di libertà addizionali, è stato usato per analisi di stabilità e vibrazioni di telai in FRP (Minghini et al. 2009, 2010).
L'efficacia del modello FE-BIE è illustrata in questa nota attraverso due esempi riguardanti sottovie in c.a., nei quali l'ipotesi di substrato lineare elastico è giustificata dal limitato livello tensionale raggiunto sul piano di fondazione.
Risultati preliminari ottenuti con il modello qui adottato sono stati presentati da Baraldi (2013), Tezzon et al. (2015) e Baraldi e Tullini (2017).
2 FORMULAZIONE DEL MODELLO FE-BIE
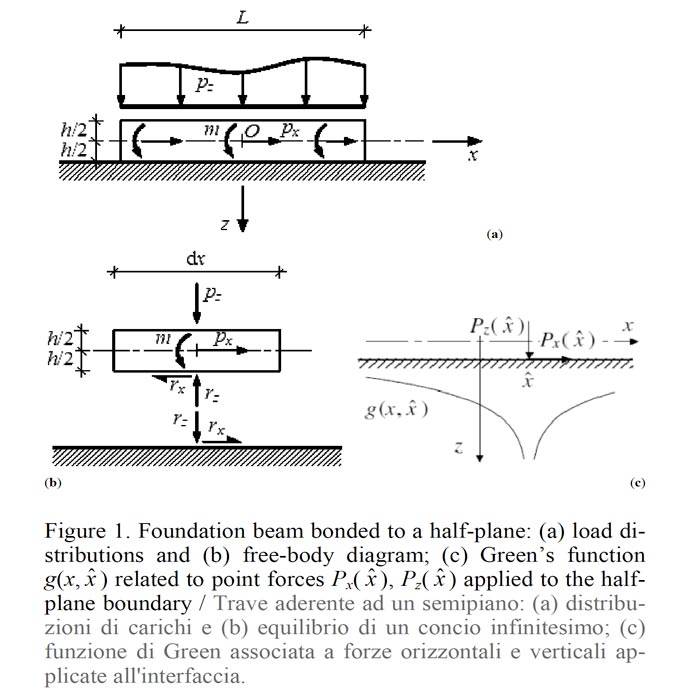
Si fa riferimento ad una trave di fondazione perfettamente aderente ad un substrato bidimensionale semi-infinito (Fig. 1a). Si introduce quindi un sistema di coordinate cartesiane (O; x, z), dove x coincide con l'asse baricentrico della trave e l'asse z è orientato verso il basso. La trave ha lunghezza L e altezza h. Pertanto, l'interfaccia fondazione-substrato si trova alla quota z = h/2. Si assume poi uno stato piano di tensione o di deformazione.
Nel secondo caso, la larghezza b della sezione trasversale è unitaria tanto per la trave quanto per il semi-piano.
Nelle analisi si adottano spostamenti piccoli e deformazioni infinitesime. I materiali di trave e substrato sono ipotizzati omogenei, elastici lineari e isotropi.
Nel seguito, le constanti Eb e νb saranno usate per indicare, rispettivamente, il modulo di Young ed il coefficiente di Poisson della trave, mentre Es e νs
indicheranno il modulo di Young ed il coefficiente di Poisson del substrato. L'asse della trave è soggetto a distribuzioni di carichi orizzontali e verticali px(x) e pz(x), e di coppie m(x). L'ipotesi di perfetta aderenza comporta lo sviluppo di tensioni tangenziali, rx(x), e normali, rz(x), all'interfaccia (Fig. 1b).
...
L'ARTICOLO COMPLETO E' DISPONIBILE IN ALLEGATO
KEYWORDS: RC tunnel; soil-structure interaction; plastic hinge; elastoplastic analysis; mixed finite element / sottovia in c.a.; interazione suolo-struttura; cerniera plastica; analisi elastoplastica; elemento finito misto
Articolo presentato in occasione degli Italian Concrete Days 2018 di aicap e CTE

ITALIAN CONCRETE DAYS - L'Evento più importante per gli appassionati di strutture in Calcestruzzo
Dal 14 aprile al 17 aprile 2021 si terrà la terza edizione degli Italian Concrete Days. Ulteriore informazione sull'evento a questo LINK.



