Analisi di telai su semispazio elastico mediante un approccio FE-BIE
Il presente lavoro riguarda lo studio dell’interazione suolo-struttura attraverso un approccio di tipo FE-BIE. Il problema d’interazione viene studiato servendosi dell’accoppiamento tra il metodo agli elementi finiti, per il calcolo delle sollecitazioni sulla struttura, e equazioni integrali al contorno, utilizzate per descrivere la risposta del sottosuolo elastico e isotropo.
La formulazione è validata attraverso un confronto con la soluzione numerica ottenuta tramite la modellazione di un opportuno volume di terreno con elementi finiti solidi.
Viene quindi presentata un’applicazione relativa ad una struttura intelaiata con fondazioni superficiali su suolo elastico, utile ad evidenziare la necessità di una modellazione tridimensionale del problema. La variazione delle caratteristiche del sottosuolo ha permesso di indagare nel dettaglio il diverso comportamento delle strutture in termini di sollecitazioni e reazioni del terreno.
I problemi di contatto tra elementi strutturali e substrati elastici interessano diversi campi: geologia, ingegneria, aeronautica, rinforzo strutturale in FRP
L’interesse per i problemi di contatto tra elementi strutturali e substrati elastici è rilevante in diversi campi come: geologia, ingegneria, applicazioni aeronautiche, rinforzo strutturale in composito FRP. Le soluzioni analitiche al problema sono ristrette ai casi dell'indentatore rigido e della trave di lunghezza infinita su semispazio elastico, isotropo o anisotropo (Johnson 1985, Kachanov et al. 2003).
Nel corso degli anni la necessità di studiare problemi di interazione suolo-struttura ha portato all’adozione di semplici modelli di suolo come il modello di Winkler e quello di Pasternak basati sulla proporzionalità tra pressione e spostamenti verticali in tutti i punti della superficie di contatto (Selvadurai 1979). Riguardo ai modelli numerici, l'interazione suolo-struttura è stata analizzata in passato mediante vari approcci. In uno di questi (Selvadurai 1979) si fa uso del metodo degli elementi finiti (FEM) per discretizzare sia la fondazione sia il substrato.
Tale approccio, pur consentendo di descrivere geometrie complesse, comporta spesso un eccessivo onere computazionale, in quanto la mesh del substrato deve essere estesa ben oltre i confini della superficie caricata per garantire, lontano dai carichi, le condizioni di suolo indisturbato. L'uso di elementi beam per la fondazione e di elementi bidimensionali per il suolo comporta la perdita della continuità delle rotazioni all'interfaccia. Storiche formulazioni di semispazio elastico per l’interazione suolo-struttura sono dovute a Cheung e Zienkiewich (1965) e Cheng e Nag (1968).
Essi hanno sviluppato un modello per l’analisi di travi e lastre appoggiate su una fondazione elastica che incorpora la soluzione di Boussinesq. Uno strumento particolarmente vantaggioso per l'analisi di semispazi elastici è rappresentato dal Boundary Element Method (BEM), che consente di discretizzare solo l'interfaccia con la sovrastruttura (Ribeiro & Paiva 2015). Tuttavia, le reazioni del suolo vengono tipicamente considerate come reazioni nodali nel modello agli elementi finiti della sovra- struttura e quindi, anche in questo caso, si perde la continuità delle rotazioni all'interfaccia.
Inoltre i modelli citati richiedono l'inversione esplicita della matrice di flessibilità del substrato. Kikuchi (1980) ha introdotto per la prima volta una formulazione variazionale che include un'opportuna funzione di Green per il suolo.
Bielak e Stephan (1983) hanno studiato la flessione di travi su suolo elastico usando una funzione di Green derivata dalla funzione di influenza di Boussinesq. Il problema discusso da Tezzon at al. (2015) si riferisce a carichi applicati alla superficie del suolo di un semispazio elastico bidimensionale in stato piano.
Nello studio, l’accoppiamento Finite Element-Boundary Integral Equation (FE-BIE) è usato per l’analisi dello stato piano di tensione o di deformazione di travi e telai vincolati a un semi-spazio bidimensionale elastico isotropo ed omogeneo. Il mo- dello fa uso di una formulazione numerica standard della trave basata su spostamenti, accoppiati con equazioni integrali per descrivere la frontiera del substrato che include un’opportuna funzione di Green.
Le variabili indipendenti della formulazione sono lo spostamento e la rotazione della trave e le tensioni superficiali del suolo nella direzione tangenziale e normale. Solo la trave a contatto con il terrno deve essere discretizzata. Diversamente dalle formulazioni disponibili in letteratura, il modello proposto impone la continuità delle rotazioni tra la trave di fondazione e la frontiera del semi-spazio nei nodi.
Un modello analogo è stato usato da Tullini e Tralli (2010) e Tullini et al. (2012, 2013a, b). Tale formulazione conduce ad una matrice simmetrica per il substrato, permettendo così di evitare gli inconvenienti legati alla non simmetria della matrice dei coefficienti del BEM.
Infine, la matrice risolvente del modello ha dimensioni proporzionali al numero di elementi finiti della fondazione. Al contrario, nel FEM un raffittimento della mesh conduce ad una matrice di rigidezza di dimensioni pari a diverse volte il quadrato del numero di elementi usati per la fondazione.
Formulazione del modello FE-BIE
Si fa riferimento ad una trave di fondazione in contatto, privo di attrito, con un substrato tridimensionale (Figure 1). Si introduce un sistema di coordinate cartesiane (O; x, y, z), dove x coincide con l’asse baricentrico della trave, y è disposto sulla sezione trasversale della trave e z è orientato verso il basso.
La trave ha lunghezza L, base B e altezza h. L’interfaccia fondazione-substrato si trova a quota z = h/2. Nelle analisi si adottano spostamenti piccoli e deformazioni infinitesime. I materiali di trave e substrato sono ipotizzati omogenei, elastici lineari e isotropi. Nel seguito, le constanti Eb e νb saranno usate per indicare, rispettivamente, il modulo di Young ed il coefficiente di Poisson della trave, mentre Es e νs indicheranno il modulo di Young ed il coefficiente di Poisson del substrato. L'asse della trave è soggetto a distribuzioni di carichi verticali pz(x) e di coppie m(x). L'ipotesi di assenza di attrito tra trave e substrato comporta lo sviluppo di sole tensioni normali, rz(x), all'interfaccia.
Energia potenziale totale del sistema
Lo spostamento verticale w di un punto della frontiera sottoposto ad una generica reazione 𝑟(𝑥̂,𝑦̂) è dato dalla soluzione di Boussinesq:
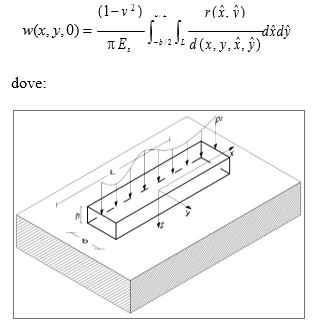
FIGURA 1: Trave con sezione rettangolare su semi-spazio elastico.
... CONTINUA LA LETTURA NEL PDF ALLEGATO
La presente memoria è tratta da Italian Concrete Days - Aprile 2021
organizzati da aicap e CTE
SCARICA L'ARTICOLO COMPLETO IN ALLEGATO
