Affidabilità strutturale degli edifici esistenti e Indice di Cornell

Con questo articolo si vuole fornire una introduzione di base all’argomento, in modo da favorire la comprensione di questi concetti, concetti che caratterizzeranno sempre più le analisi strutturali, attraverso le prossime modifiche normative, come è stato recentemente confermato dal Prof. Braga, in una intervista realizzata in occasione del Convegno ANIDIS 2022 con particolare riferimento agli edifici esistenti.

 
Funzione dello Stato Limite e probabilità di crisi

Che cosa è l'affidabilità strutturale

L'affidabilità strutturale è una quantificazione a carattere probabilistico della sicurezza, e viene definita come capacità di una struttura o di un elemento strutturale di soddisfare i requisiti di prestazione specificati nelle condizioni prefissate durante il tempo prescritto.

In altri termini: capacità di una costruzione di assolvere alla funzione per cui è stata concepita durante l’intero periodo temporale per cui deve funzionare, mantenendo il prefissato livello di sicurezza.

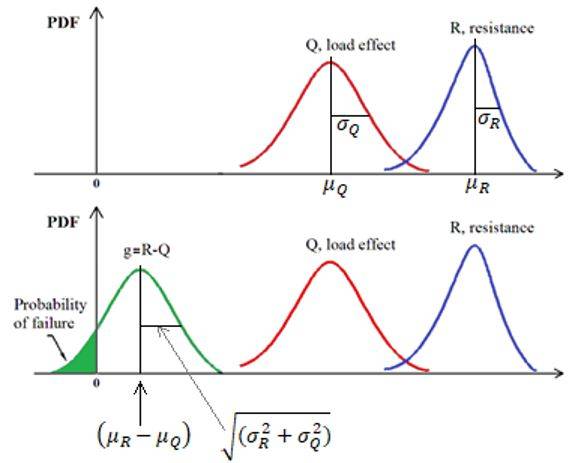
La formulazione fondamentale del problema coinvolge la resistenza R e l’effetto del carico Q (spesso indicato anche con i simboli E, effetto o S, sollecitazione): queste grandezze, da intendersi in senso generalizzato, vengono descritte dalle rispettive funzioni di densità della probabilità.

In generale, sia Q l’effetto del carico in un elemento strutturale e R la sua resistenza: allora la funzione di stato limite g può essere espressa come:

g = g(R,Q) = R-Q

Se l'effetto del carico supera la resistenza, l’elemento strutturale supera lo stato limite e si definisce la probabilità di superamento dello stato limite P_f nel seguente modo:

P_f = P(g<0)

Sia la resistenza R che l'effetto del carico Q sono variabili casuali, ossia affette da incertezze relative a molti aspetti: comportamento dei materiali, entità dei carichi, modellazione della struttura su geometria, posizionamento dei carichi e vincoli, modelli matematici utilizzati.

Ciascuna ha la propria funzione di densità di probabilità (detta anche: funzione di distribuzione della probabilità) PDF che esprime la probabilità che la misura della grandezza in esame assuma un determinato valore.

Anche g è quindi una variabile casuale e viene caratterizzata dalla propria funzione di densità di probabilità; è così possibile calcolare la probabilità di superamento dello stato limite.

Supponendo che la resistenza R e l’effetto del carico Q siano entrambe variabili aleatorie con distribuzione normale, allora anche la funzione del margine di sicurezza g(R,Q) = (R-Q) ha distribuzione normale con valore medio (μ_R-μ_Q) e deviazione standard √(σ_R^2+σ_Q^2).

In figura seguente sono riportate le tre distribuzioni R, Q e g, con i rispettivi valori medi e deviazioni standard.

La probabilità di superamento dello stato limite è data dall’integrale della funzione di distribuzione di g da -∞ a 0:

P_f = P(x≤0) = ∫_-∞⁰ g(x) dx

Attraverso la funzione di distribuzione di probabilità cumulativa Φ, questo integrale può essere espresso utilizzando per le variabili X, μ, σ i seguenti valori: X = 0, μ_g = (μ_R-μ_Q ), σ_g = √(σ_R^2+σ_Q^2) da:

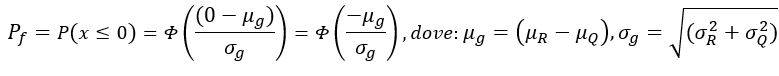
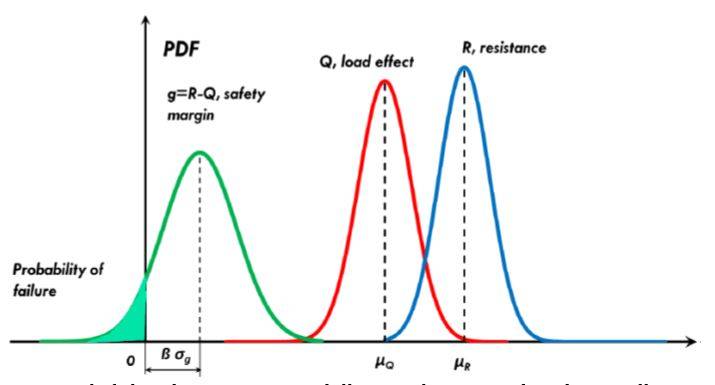
Cornell ha definito il coefficiente β pari al rapporto tra μ_g e σ_g:

β = μ_g / σ_g (indice di affidabilità, o indice di Cornell)

L’indice è graficamente rappresentato nell’immagine seguente, dove risulta evidente che β è la frazione di deviazione standard corrispondente al valore medio: βσ_g = μ_g .

L’espressione della probabilità di superamento dello stato limite diviene quindi:

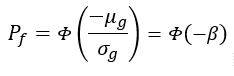
L’indice di Cornell è dato da:

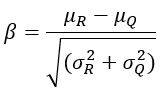
Pertanto, se R e Q sono due variabili indipendenti con distribuzione normale, caratterizzate da μ_R σ_R e μ_Q σ_Q, si calcola l’indice di Cornell e si ottiene la probabilità di superamento dello stato limite:

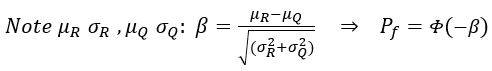
Risulta che più è elevato l’indice di affidabilità, minore è la probabilità di superamento dello stato limite (graficamente, minore è l’area colorata in figura sopra) e quindi il rischio associato a questo caso sarà meno elevato.

La probabilità viene generalmente espressa nel formato 10ⁱ, come nella tab.C1 dell’EuroCodice EN1990, che fornisce i valori di β per probabilità comprese fra 10^-1 e 10^-7.

Le probabilità più utilizzate in ingegneria civile sono 0.001=0.1% (10^-3), 0.01=1% (10^-2), 0.1=10% (10^-1).

 
Affidabilità di una struttura esistente

Nell’ambito dei metodi probabilistici, viene qui presentato un lavoro di Croce et al.¹ relativo alla calibrazione dei fattori parziali per le valutazioni di edifici esistenti in muratura, dove una procedura innovativa costituisce un’importante base di sviluppo verso la conoscenza delle proprietà dei materiali.

E’ stato analizzato un database di risultati di prove in situ raccolti dagli autori su insiemi piuttosto omogenei di edifici in muratura di mattoni e pietra situati nella stessa area geografica, proponendosi l’obiettivo di una classificazione razionale dei vari tipi di muratura, fornendo, allo stesso tempo, valide informazioni sulle proprietà statistiche dei parametri meccanici.

In base ai risultati delle indagini, sono stati determinati i parametri statistici caratterizzati da media e deviazione standard per alcuni parametri meccanici significativi, quali la resistenza a compressione ed i moduli di elasticità E e G. Come atteso, sono risultati dati caratterizzati da un’elevata dispersione (elevato coefficiente di variazione COV), determinata dall’ampia variabilità delle caratteristiche della muratura anche per edifici della stessa tipologia, relativamente alla qualità della malta, alla forma e alle dimensioni degli elementi lapidei, alla tessitura muraria, allo stato di degrado.

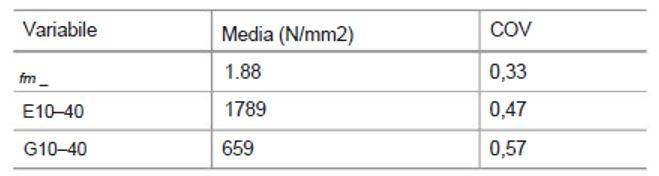
I risultati ottenuti evidenziano l’esistenza di classi diverse all’interno della stessa tipologia muraria.

Si è quindi effettuata un'ulteriore analisi per identificare popolazioni statistiche omogenee per i parametri meccanici della muratura.

E’ stata applicata la tecnica della miscela di curve gaussiane GMM (Gaussian Mixture Models) in grado di individuare n sottopopolazioni statistiche omogenee, ognuna caratterizzata da una distribuzione normale con dispersione minore rispetto a quella della popolazione completa. Si è scelto n=3 per suddividere le murature in 3 classi: alta qualità, media qualità, qualità scarsa.

In figura sopra è riportata la distribuzione di probabilità per i valori ottenuti per la resistenza a compressione, con ipotesi di distribuzione normale (curva in blu scuro) e lognormale (curva in rosso). Nello stesso grafico, sono riportate le distribuzioni di probabilità normali delle 3 classi di muratura, ottenuta attraverso la tecnica GMM di identificazione delle sottopopolazioni.

Si ottengono così i valori medi e le deviazioni standard per ognuna delle 3 classi murarie, e i corrispondenti coefficienti di variazione sono tutti inferiori a quello ottenuto considerando la popolazione completa.

Riduzione delle incertezze nella valutazione statica e sismica

L’esperienza illustrata in da Croce et al. suggerisce un approccio innovativo in grado di migliorare notevolmente i valori dei parametri di resistenza adottati per i materiali murari. Si delinea così un possibile percorso di progettazione per i professionisti.

Analizzando un particolare edificio, viene in genere previsto un certo numero di prove (anche limitato) per la definizione dei parametri meccanici. L’integrazione dei valori ottenuti con i risultati di elaborazioni statistiche disponibili per tipologie coerenti con l’edificio in esame renderà possibile definire valori di progetto delle resistenze e dei moduli elastici correttamente calibrati.

Questo percorso conduce verso un importante obiettivo: la riduzione delle incertezze nella valutazione delle prestazioni statiche e sismiche degli edifici esistenti.

L'ARTICOLO COMPLETO NEL PDF

¹ Croce P., Beconcini M.L., Formichi P., Landi F., Puccini B., Zotti V., ”Evaluation of Partial Safety Factors for the Structural Assessment of Existing Masonry Buildings”, 2021.